
	Advertisment

Maximum Jeopardy!

I like to watch Jeopardy! The other night I was wondering just how much money it’s possible, theoretically, to win in a single game.

The Game

There are three rounds in a Jeopardy! Game: The Jeopardy Round, Double Jeopardy and Final Jeopardy.

To calculate the highest possible score, it’s assumed that you ring-in first and correctly answer each question, beating out both opponents. If you need a summary of the full rules of the game, read this article.

The Jeopardy Round

In the first round, there are six categories, each with five different scoring questions: $200, $400, $600, $800, $1000.

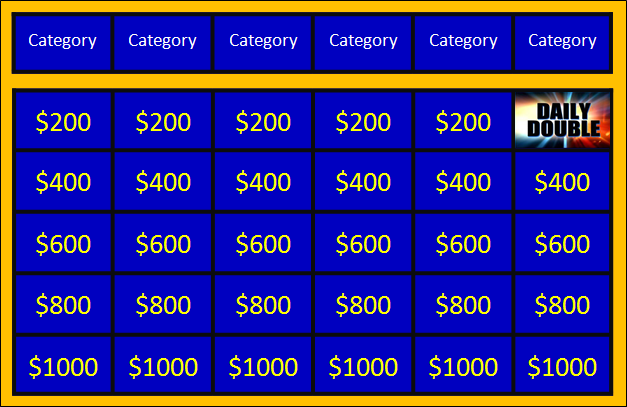
It does not matter what order the questions are answered in, however there is a subtlety in that one of the squares (selected at random by the show creators) is the Daily Double square. When this square is revealed, the contestant can wager any dollar value up to his current balance (or up the value of the highest question on the board; whichever is the highest).

Successfully answering the Daily Double question earns the player the amount of their wager, allowing them to, potentially, double up their score (failing to answer the question loses the player their entire wager).

Clearly, to maximize our score we’d want our player to have earned the highest possible score before answering the daily double question, and to maximize our score the following requirements need to be met:

	The daily double square must be the last question answered.
	The player needs to wager all the money he/she has.
	The Daily Double square needs to be have been found under a $200 square ^*

^* When a daily double is encountered, the player does not obtain the cash value depicted on the square, instead he wagers. Thus, by having the Daily Double under the lowest cash value square, we maximize our earning potential of cash before being allowed to double up.

Scoring on the Jeopardy! Round

There are five complete categories with questions: $200, $400, $600, $800, $1000, giving a total of 5 x ($200 + $400 + $600 + $800 + $1000) = $15,000

Next, there is one category with: $400, $600, $800, $1000 questions for a total of $2,800. The total maximum score a player could obtain, before the Daily Double square is encountered is, therefore, $17,800. If our player then bets it all on the last question this round he would finish the Jeopardy! Round with a score of $35,600

The Double Jeopardy! Round

The Double Jeopardy! Round is very similar to the Jeopardy! Round with just two small differences: The first is that all point values are doubled, and the second is that this round contains two Daily Double squares.

As before, to maximize our score we need to answer all the vanilla questions before revealing the two Daily Double squares. These squares need to be the last two squares, and also need to have been placed under $400 question squares (the lowest scoring squares on the board).

Scoring Double Jeopardy!

There are four complete categories with questions: $400, $800, $1200, $1600, $2000, giving a total of 4 x ($400 + $800 + $1200 + $1600 + $2000) = $24,000

There are two partial categories with questions values of $800, $1200, $1600, $2000, giving a total of 2 x ( $800 + $1200 + $1600 + $2000) = $11,200

So, adding in the score from the Jeopardy! Round, before answering the first of the Double Jeopardy! Daily Double the player would have a score of: $35,600 + $24,000 + $11,200 = $70,800

Successfully answering the two Daily Double questions will bring the score, at the end of this round, to $70,800 x 2 x 2 = $283,200

Final Jeopardy!

The last question of the game allows a player to wager, again, anything up to his current score. So, by wagering his entire $283,200 the player can double up one more time to get final score of $566,400

$566,400

The highest achievable score in a single game of Jeopardy!

~~(At the time of writing this article, the highest single day score achieved in a game of Jeopardy! Is $77,000 by Roger Craig, in 2010).~~

UPDATE - On April 9th 2019, contestant James Holzhauer, achieved a new single day score record by earning $110,914.

UPDATE #2 - On April 17th 2019, contestant James Holzhauer, achieved a new single day score record by earning $131,127.

Well done James!

So how likely is this?

Clearly a situation like this is contrived: The Daily Doubles needing to be found last of all (and each occurring under the lowest value squares). Also, you’d need a player with a super-human level of confidence to play a strategy like this … or would you?

Imagine, for a second, that you are a good Jeopardy! player. Midway through the first round it’s probably pretty clear to everyone that you are dominating your two opponents. If you’ve been able to answer all the questions to-date, unchallenged, it’s pretty obvious there is a strong measure of skill asymmetry in this game. If you get to the last question unopposed, why not gamble all on the Double Jeopardy! question? What’s the worst that could happen?

If you get it wrong, no big deal, you’ll drop to zero points and by tied with the other two players. The next round is Double Jeopardy! and, since you are playing against intellectual dolts, in no time at all you’ll be monopolizing the answers again. (Also, typically, questions in Jeopardy! get harder as the point values increase, and so if the Daily Double was found under the $200 square, the implication is that the Daily Double question should be the easiest question of a category you have already dominated). Why not bet it all?

A similar argument can be applied to the Double Jeopardy! round. In our scenario you would have had to answer every question correctly to get to the two final Double Jeoprady! Questions. Why not bet it all? Past history is on your side that you are smart (having answered all the previous 58 questions correctly), and there is no time pressure in answering the last two questions (Daily Double questions are not Ring-in questions, you don’t compete with anyone else, all you have to do is answer).

Again, what is the worst that could happen? If you lose it all, you’d be tied with the other two opponents at zero points. In Jeopardy! if there is a tie, then all these people return to play again the next day. If you messed up, yes, you’d miss out on the big payday, but the downside is that you get to return the next day and compete against the same opponents (which past-performance shows that you dominate), and you can have another crack at going down in Jeopardy! history.

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.