How to escape a monster
It’s getting close to Halloween, here’s a monster puzzle:
Imagine you are sitting in a rowing boat in the middle of circular lake. Standing on the edge of the lake is a hungry monster. The monster wants to eat you. You want to escape.
You know that, if you can reach land, you can outrun the monster, but first of all, you need to row to shore. Here’s the issue: whilst you can outrun the monster on foot, he can run faster than you can row the boat. Much faster. The monster can run four times faster than you can row. He’s also a clever monster and will always do that smartest thing to attempt to catch you; moving around the shoreline, as needed, to maximize his advantage. If he touches you, you’re dead!
Can you escape?

Impossible?
|
I have to admit, when I first heard this puzzle, my initial thought was that it is impossible to escape. Let's imagine you made a direct dash for the shore directly opposite where the monster is currently standing. The radius of the lake is R. The speed you can row is v. The distance to the shore is simply the radius, so the time taken to get to shore is R/v. The monster, seeing you are making a dash for the shore, will sprint around the edge of the lake. It does not matter which direction he runs, and he will end up running half the circumference. The distance he will run is πR, and running at speed 4v, he will get to your landing point after just πR/4v. As we know that π is less than four, we can see that the monster will get there first. He’s going to eat your brains if you use this strategy! Towards the middle or end of your dash, once you realize the monster is closing, even if you adjust your strategy to add some tangential component, you're screwed. The faster speed of the monster means he can always catch you. We need a better strategy … |
 |
Smarter Strategy
Rowing in straight line is clearly the correct strategy (if you rowed on a curved line, you'd end up at a location that you could have gotten to quicker with a straight shot). However, we've shown that starting at the center results in failure.
To solve this puzzle, what we first need to do is calculate the position from which a radial sprint to the shore will result in victory (we'll worry about how to get into this position in step two).
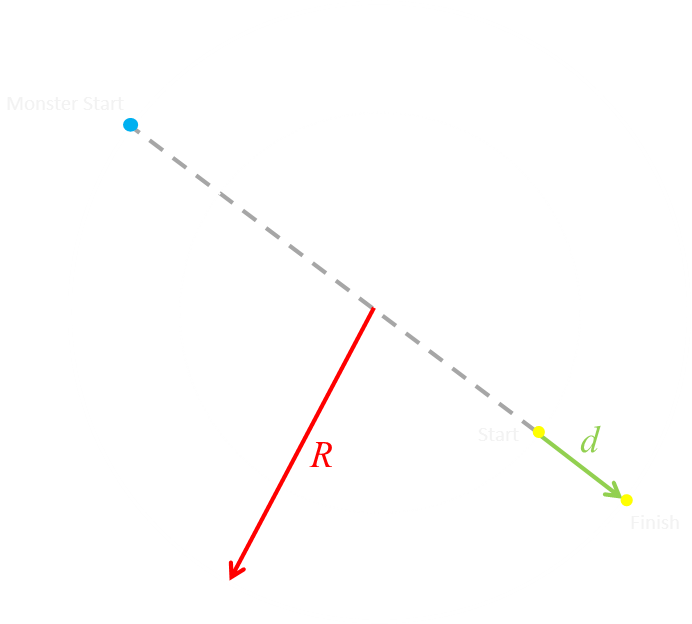
There's an annulus (ring) at the edge of the lake in which, if we start inside, and sprint directly towards the shore we be sure of escape. Taken to the limit, in the diagram above, we can see that if we start with the monster diametrically opposed to us there is a maximum value for d.
We know that the monster needs to run half the circumference of the lake, and the time this will take him is πR/4v. In this same time, we must row the distance d. At the limit, the time taken to complete these distances will be the same, so πR/4v = d/v, so we can calculate the maximum value of d = πR/4. If we start any closer to the center of the lake than this point, the monster will catch and eat us.
Using a calculator we can find out that d = 0.7854R
Getting to the escape point
Now all we have to do is work out how to get to this escape point (on the edge of this annulus with the monster opposite us).
When we are close to the center of the lake, we can row in tight circles. If the circle is small enough (less than a quarter of the radius of the lake), we travel radially around the lake faster than the monster can. We can use this to position ourselves relative to the monster at any arbitrary location (In this case, 180°).
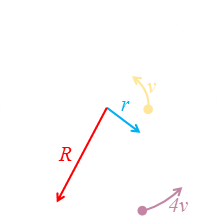 |
Starting from the middle, we can row in a spiral, slowly increasing our radius and, providing we stay at at radius r < R/4, we can always move faster than the monster and thus be able to make sure we position ourselves at 180° away from him. Once we have manoeuvred ourselves to a position d away from the edge, with the monster opposite, we can use the escape plan described above to escape. We know that d = 0.7854R, so this corresponds to a radius of r = (R - d), which gives a value r = 0.2146R This is great news because we know we can stay ahead of the the monster until a radius of r = 0.25R (travelling a quarter as slow allows us to navigate circles up to a quarter the circumference of the lake). |
So now we have our solution: We can spiral out until we reach a radius of 0.2146R < r < 0.25R with the monster opposite us, and be sure of an escape! Hurrah for math!
What about a faster monster?
 A faster monster |
We've shown that we can outsmart a monster that can run four times as fast as we can row. The inequality above, however, shows that we have some headroom. What is the fastest monster we can escape? To calculate this, we need a little more math* … The fastest monster we can escape is determined when the monster arrives at the shore at exactly the same time we do. Let's define the ratio of our two speeds by the letter K. (The monster runs K-times faster than we can row). What is the maximum value for K? *Actually, quite a lot more math! |
Hold on, here comes the math …
|
The first part of the puzzle stays the same. We know that, in a tight circle, we can row with a higher angular velocity than the monster can run. If we are inside this circle we can position the monster to any arbitrary angular position relative to us. (In fact, if we adopt an optimal strategy, and move outwards at full speed, always keeping the monster co-linear with the center of the lake, the path we follow is a semi-circle of radius R/2K). The radius of this circle of safety is determined by the ratio of the two speeds. It’s radius is R/K. The monster is a smart monster (as well as being hungry, he has an advanced degree in mathematics from Monster’s University), so he knows that, once you cross outside the circle of safety he has a higher angular velocity, so as soon as he sees you leave the circle, he sprints at full speed to your side of the lake. (It’s obvious he needs to do this, if not, he’s giving you the advantage of being able to get further away!) |
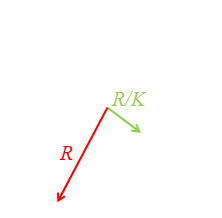 |
 |
Similarly, once the monster has committed to the direction he’s going to run around the lake, it would be foolish for him to change direction. If he did, he’d re-pass the point he was previously at, but now you’d be closer to the shore! We already know that you should always row in a straight line (anything else just wastes time), and that the monster is committed to his run. The question is: should we simply dash for the shore (as in the simple solution above), or can we gain advantage at aiming at little further around the shore? Sure, the straight shot to the shore is the shortest distance, but is it possible to row a slightly longer (straight) route to the shore if it would require the monster to run further to catch you? As long as the extra time it takes you to row this extra distance is less than it would take the monster to run to the same point, you are better doing it. |
In the diagram below, I've plotted out a couple of possible paths. Path #1 is the strategy from our simple solution. It is the shortest distance from the edge of the safety circle to the shore. Can we do better?
Path #2 is a example of a generic path from the circle of safety to the shore. Yes, it's longer, but the monster also has to run longer. As the monster is committed to its run, it needs to continue around the edge of the lake to you.
At the limit is Path #3, which is a tangent to the circle of safety. Anything past this, like Path #4 takes us back inside the circle of safety and would result in new solution being required when we exited the other side (and you'd essentially have to start the process again, otherwise, if you didn't, as soon as you went inside the circle, if you did not manoeuvre the monster opposite you again before starting your dash to shore, you would give him an advantage). The solution can not occur 'West' of Path #3 (if we define 'North' as vertically upwards).
We can, therefore, reject Path #4, and the solution must lay somewhere between Path #1 and Path #3 inclusive.
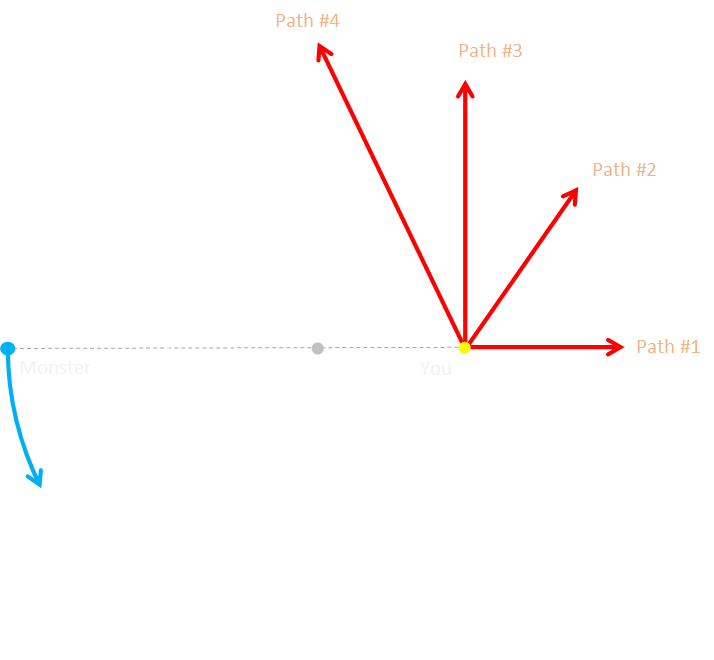
Note: It should be very obvious that the optimal solution does not occur 'South' of Path #1. Anything below Path #1 takes you towards the monster !!!
More math …
OK, we're now going to break out some trigonometry. If you're squeamish about math, you're going to want to skip to the answer section. It's only going to get worse from this point onwards …
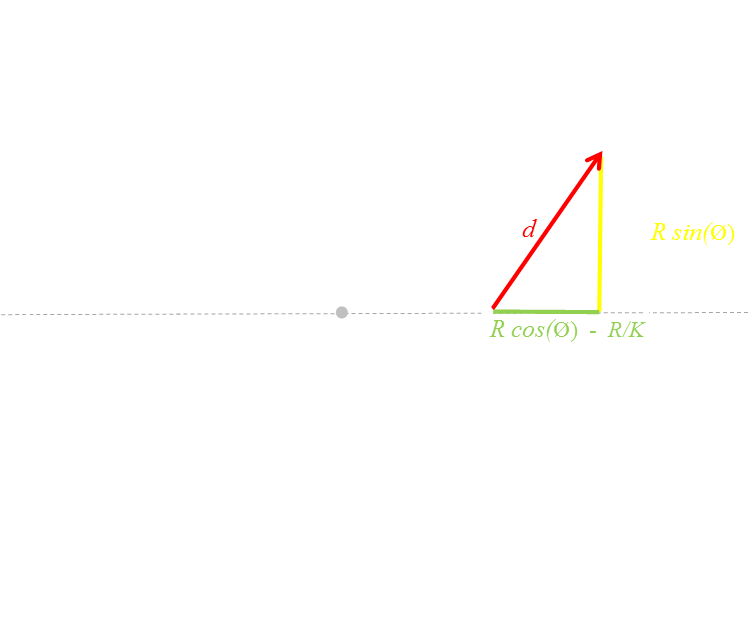
The distance we row from the exit point of the circle of safety to the shore, we'll call d. This value can be calculated using Pythagoras and the right hand triangle colored in the image above.
Expanding this out we get this:

Do you remember your trig equalities? Here's one we will be using a lot today: sin2 + cos2 = 1
Using this equality we can simplify the equation to this:
|
In the diagram on the right we can see that the monster has to run the blue route, which goes past halfway, and continues along to the interception point. The distance the monster needs to run we'll call m :
(We are using radians for the angles) The puzzle reduces down to the following questions:
|
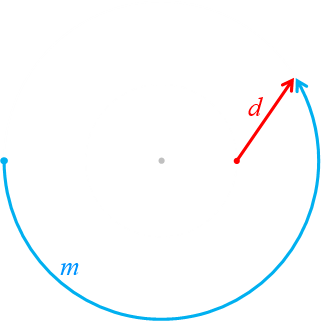 |
For you to escape, the time taken to row distance d, needs to be less than, or equal to the time it takes the monster to run m.
The limit will be reached when both you and the monster arrive at the same point at the same time.
 |
If you both arrive at the same time, and you rowed a distance of d, the monster, who runs K times faster will have run K times the distance. The equation on the left is another way to describe the value d. |
Squaring this, we can equate it to the representation of d2 derived by Pythagoras.
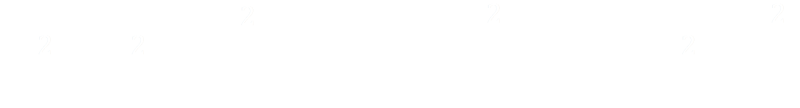
To simplify, first we multiply both sides by (K/R)2 … bear with me, you'll see why …
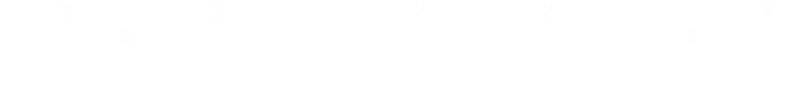
This can be simplified to:

Adding, and subtracting cos2 from the left side allows the terms to be simplified into a square expression:

Then, using the trig equality again in the form: 1 - sin2 = cos2 gets us to here:

Finally, rearranging we get our first important result:
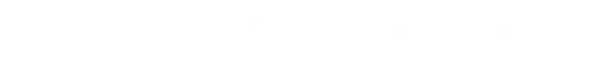
This is awesome. It gives us the relationship between K and Φ
Calculus
OK, we're onto the home straight, but now we need to break out our Calculus. Maximum (and minimum) points occur at points where first derivatives are zero. We need to derive the first derivative of K with respect to Φ
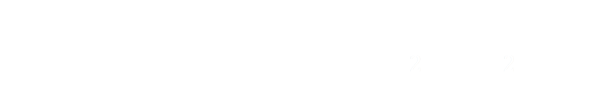
We want to find the value of Φ when dK/dΦ = 0. With a little rearranging we get this:
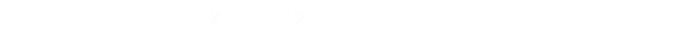
Next we square both sides:
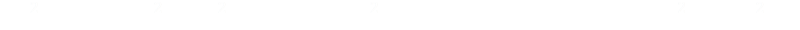
Things have to get a little worse before they get better. Here we move things around and regroup:

Applying our old friend the trig equality sin2 + cos2 = 1 once again:
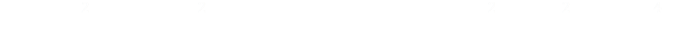
Next we divide by sin2. Remember from school that cos / sin = cot …
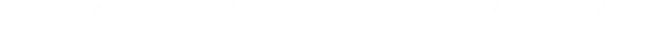
For one last time we'll use sin2 + cos2 = 1:
Oooh, look, the above is a perfect square, and simplifies nicely:
And now we have our solution!
This equation can be solved with your favourite tool (graph paper, Excel, Newton-Raphson, trial and error, calculator, abacus …) and yields a value of Φ ≈ 1.35181680431927…
We can plug this value back into our first result

The results
|
The maximum value for K is 4.6033388489… That's right, we can outrun a monster that can run just over 4.6x the speed we can row!
|
 A 4.6x faster monster! |
But which way should you row?
We now know how fast a monster it is possible to evade. We also know what angle from the center of the lake this corresponds to, but what angle do we depart circle of safety from? Let's find out …
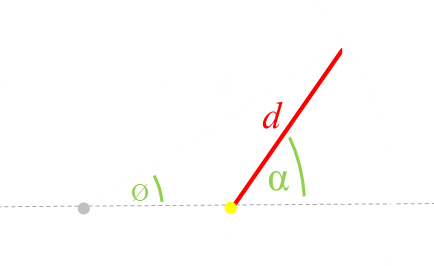 |
We'll call the angle the boat should take from the collinear line as α From simple geometry can see the relationship between the two angles because they are both right-angle triangles and share a common side.
|
|
From our earlier results, we know the relationships between d, R,Φ and K The top two equations on the right, which we derived earlier, can be combined.
|
 |
 |
This last equation can be rearranged to given an alternative form of R sin(Φ) which we can insert into the equation derived from the geometry. |
And here we have it:
That's right, the angle you should row your boat is 90° from the collinear line! It's a tangent to the circle of safety. It's what we called Path #3 earlier.
Summary
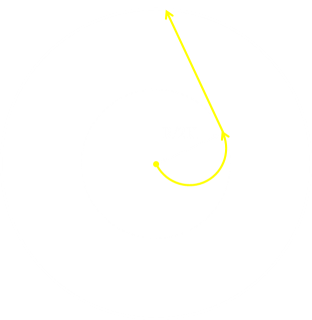 |
If you ever find yourself in the middle of a circular lake with monster who can run less than 4.6033388489 times as fast as you can row, then row outwards and around on a semi-circular path of radius R/2K until you reach a radius of R/K, then continue straight on until you reach the shore, and escape. The path you will follow will resemble a letter 'J'. The original author of this puzzle, I believe, is none other than Martin Gardner. If you like this puzzle, you might like some of these. |
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.