Amidakuji
|
When I was growing up there was a popular video arcade game called Amidar. This game was vaguely similar to Pac-Man. On the odd numbered levels of this game the player would move on a lattice collecting coconuts whilst avoiding bad guys. Collecting all the coconuts around any rectangle filled in that rectangle, and when the four corners were filled in the tables could be temporarily turned on the bad guys (just like eating a power-pill in Pac-Man). In addition, the player had a limited number of jumps which bounced and confused the bad guys for a second allowing the player to dash past. Once all the coconuts were collected, the round ended. |  |
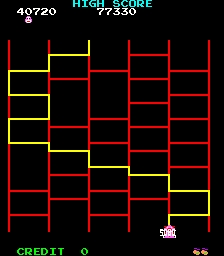 |
Even numbered rounds followed a slightly different format and this time the player controlled a paint roller. The mechanic was very similar, but instead of collecting coconuts, the player painted the perimeter of the rectangles with the paint roller.The additional challenge was that each fresh rectangle painted had to be connected to one of those already painted (and only one new rectangle could be painted at once). Inbetween each level was a Bonus Round (shown left) In this bonus round, a 'random' ladder was rendered (vertical lines, sparsely connected with random short cross-braces). At the bottom of one of the verticals was a bonus score. In a limited time, the player had to select which of the top starting locations would lead them through this ladder maze to the prize. Movement of the player through the ladder maze followed two very simple a fixed rules: |
The player always moves down unless there is a horizontal junction (rung).
When a horizontal junction is encountered, player must take this (moving to the right or left as needed).
As you can see from the above screen shot, the path taken is a deterministic zig-zag pattern. Under the same starting conditions, the same path will always be taken.
The path formed looks, to me at least, a little like the path a vertical crack might take through a cemented wall of bricks; travelling through the mortar, going down when it can, then spreading horizontally when a transition is encountered.
Ghost Ladder
These deterministic movement rules are used to create a simple lottery system for 'randomly' shuffling outcomes. These systems are popular in Asian cultures.
 |
In Chinese, they are know by the name Ghost Leg |
|
In Japanese as Amidakuji(You can see where the video game of Amidar gets its name). |

|
 |
In Korean, the translation is Ladder Climbing |
Amidakuji lottery
 |
Let's imagine you are running a lottery and you have three prizes to give away: A car, A diamond ring, and a fancy vacation. However, there are four contestants: Lucy, Nick, Sam and Zhenya. Three people will get prizes, one will get nothing. We need a way, using just pencil and paper, of determining who will get what prize. It needs to be random (we'll cover a little more of that later), fair (not open to interpretation), and we need to make sure there are no collisions (a 1:1 relationship between each player and a prize). Using the two rules described above we can construct an Amidakuji to distribute the prizes. We can write the names of each of the contestants at the top (one per vertical line), and the prizes at the bottom. Next, a collection on random rungs can be draw between the lines. Finally the lines can be traced to determine who gets what prize. In this fictitious example, Lucy gets the ring (I hope it's from Tiffany), Nick gets the car (yeah!), Zhenya gets a much needed vacation, and Sam get's nothing (Sorry Sam, better luck next time!) |
Making it 'random'
 |
There are a variety of ways to make things random. Let's imagine a slightly larger competition with six options A-F. First of all, without any cross rungs, prizes and contestants would simply short-circuit down to the bottom. Here is our first opportunity for randomness, however, if there were just two people involved in the shuffling. One person could write the names across the top of the paper in any order they choose then, using a second piece of paper, these answers could be masked out and the second person could write the prizes at the bottom in the order they select. Neither person would know the order of the others answers, so, if there was no collusion between these players, this would be random. |
But what if there was distrust between players, and/or chance of collusion?
Using the masking principle above, each person could be given the opportunity to draw random rungs on the grid, covering up their work once finished (Or, if they are really paranoid, the ladder can be constructed from six individual sub-ladders generated in private/isolation, and recombined in pre-arranged order to construct the finished ladder.)
Since every player has the option to add random rungs to the grid, even if there is collusion amongst the other n-1 players, there is nothing the majority can do to guarantee the outcome as any single person's additions can change the results of the game.
In reality, the paths get so 'chaotic' and hard for the brain to predict with even just a small number of rungs that, very rapidly, the human mind can't decompile them fast enough. Many people, when making personal decisions, for instance, simply enumerate the tops and bottoms of their ladder in the clear, then draw random lines. When they trace the paths themselves the answer is a surprise to them, even though they created the entire graph!
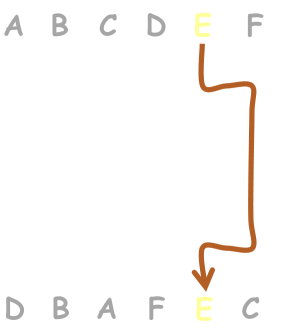 |
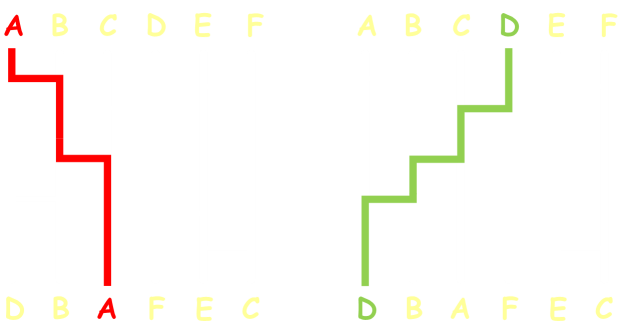
The Amidakuji has successfully shuffled the inputs and outputs. In the simple example shown in the left the order has changed from A,B,C,D,E,F to D,B,A,F,E,C As it happens, using this ladder, E stayed in the same position. That's OK, sometimes that happens and is expected and desired. It should be obvious that there can never be a collision and always a 1:1 relationship between each input and each output. (If you need help being convinced that no collisions are possible, imagine that the ladders are pipes, and you are dropping different coloured balls down each pipe; one in each pipe at the same time. The balls all fall together. Eventually two balls, at the same time, will reach the same horizontal rung. These two balls, and only these two balls, will switch places. There can be no creation or deletion of balls, so when they all fall out at the bottom, there is still just one of each color!) |
Here are some of the other paths taken:
Sensitivity to change
The addition of just one rung changes the shuffle of the matrix. It's not just which pair of verticals that are connected, it depends on the relative position of this rung to the others. Below you can see the effect on the outcome of adding one additional rung connecting C and D in three different positions.
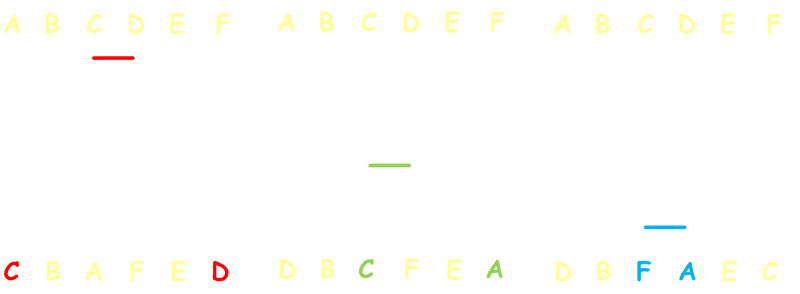
You can see how each rung switches exactly two of the outputs (think back to the ball analogy; each rung swaps the position of two balls). Which two are switched depends on the locations of the other rungs.
Reciprocity
Since the rules are deterministic, repeatable and there is a 1:1 relationship between the inputs and the outputs, a Amidakuji can be traced in reverse and the results will be consistent. Tracing the prize back up the ladder will tell you who wins that prize.
It does not matter how many rungs are added, the 1:1 relationship still holds true.
Bigger Example
Let's look at a more complicated example and learn a few more things!

|
Here is a more complex Amidakuji with twelve outcomes. Things look pretty well sorted. For this combination of rungs, however, is this the optimal configuration? Is it possible to produce the same output with fewer rungs? There are two obvious ways to solve the puzzle, the first is to start from first principles and build up the puzzle one rung at a time. The second, which we'll look at now, is to to remove redundant links from the ladder. A ladder that has the least possible number of links to give the desired solution is given the name Prime Ladder. |
Casting out pairs
|
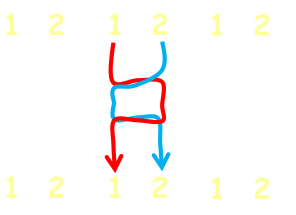
Pairs of rungs that are next to each other with no other junctions are redundant. The first swaps the path left-right, then the second reverse this right-left. It's as if they were never there. It's possible to safely remove pairs of adjacent rungs without alerting the outcome of the Amidakuji. |
 |
Below is the original ladder. On the left, the adjacent pairs have been highlighted, and the effect of their removal is shown on the right. As you can see, this de-cluttering has not altered the shuffling order.
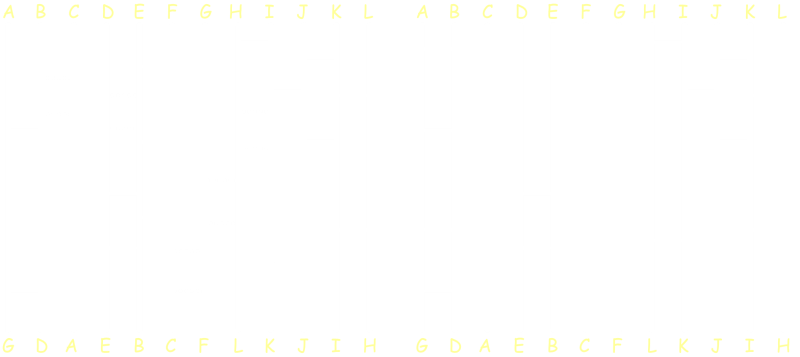
Mirror Switches
|
Slightly more complex than casting out pairs is the mirror switch. Here, if there are three adjacent vertical lines with two rungs on one side and one (intermediate) line on the other (and no other junctions between them), then it is possible to flip this around the middle line without adjusting the outcome. These two mirrored constructs are topologically equivalent. |
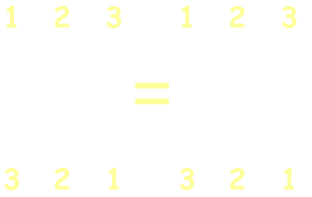 |
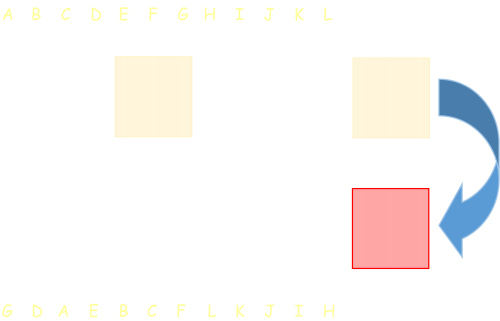 |
Applying the mirror rule to the the simplified network obtained by casting out pairs we can identify regions to switch. On the left, the region highlighted in yellow can be replaced with the equivalent region shown in red. Why would you want to do this? Well, by replacing this section with the red section, the rung on the lower right of the region now pairs up with the rung just below it. This forms a new pair we can cast out! Neat. |
|
Repeated applications of these two rules can simplify a matrix. |
|
Rock Climbing
 Image: Matthieu Lienart Image: Matthieu Lienart |
I've heard that rock climbers sometimes describe routes as Amidakuji routes. Like in the picture to the left, climbers can alternate between climbing vertically up the face, and translating horizontally along cracks and fractures as needed. Of course, rock climbers can't cast out pairs!
|
Back to Amidar
Returning to the video game Amidar, here is a video of an excellent player of the game. As we now know, the strategy to always get the bonus is to run the Amidakuji is reverse. Starting at the bonus location and moving upwards tells you where to release the character.
You may have also noticed, watching the video, that the majority* of the bad guys move in a predictable way that follows the Amidakuji path. They move up and down the board taking every horizontal turn available. Once you notice this movement pattern, it's impossible not to see it.
*The exception is the boss bad guy aka 'The Tracer', who patrols the perimeter only (for a set period of time, depending on the level). After this, he moves internally to chase the player making the game significantly harder.
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.