Friday the 13th
In urban legend, Friday the 13th is supposed to be unlucky. Enough people have such a morbid fear of this day that the condition is given a name of paraskevidekatriaphobia.
This word is derived from the Greek words paraskevi (Friday) and dekatria (thirteen) with -phobia as a suffix to indicate fear.
 Image: Attila Acs
Image: Attila Acs
|
A related term is triskaidekaphobia, from Greek tris (three), kai (and), and deka (ten), which was coined in the early twentieth century to refer to fear of the number thirteen generally. The above word forms the basis of a lexical variant friggatriskaidekaphobia, also meaning 'fear of Friday 13th'. The prefix frigga is based on the name of an ancient Scandinavian goddess who was associated with witchcraft and Friday (the witches' sabbath). “I used to be superstitious, then I heard it was unlucky, so I stopped!” |
Even un-superstitious people might admit to feeling a little uneasy when the 13th falls on a Friday.
It’s a good job this does not occur very often. Just a couple of times a year, right?
It may then, surprise you to learn that, mysteriously, the 13th is more likely to fall on a Friday than any other day of the week!
Lucky Friday 13th
|
“The 13th is more likely to fall on a Friday than any other day of the week!” |
 |
Surely, that makes Friday the 13th lucky, not unlucky! But wait, that can't be true, can it? Over a long period of time we'd expect things to average out. Is there really an affinity to Friday for the 13th day of the month? Yes, it's true. Let's prove it. But in order to do this, we need a little more background information …
(Actually it's quite a lot of background. Hold on tight!)
Here comes the sun …

|
To understand why, we have to take a step back. Modern calendar days are based on the Gregorian Calendar. What? Hold on, we have to take a further step backwards … … the Earth revolves around the Sun. Our Solar System is heliocentric. We rotate around the Sun. By definition it takes one year to go all the way around. In exactly one year we will make a complete orbit around the Sun. |
|
The Earth spins as it rotates around the sun (more on this later), and this spinning is what causes our days and nights. The axis by which the Earth spins is not aligned with the plane of rotation around the Sun, however. It's tilted approx 23.5° away from the vertical of the 'ecliptic plane'. This tilt exposes different areas of the Earth to different levels of radiation from the Sun at different parts of the orbit. (When tilted towards the Sun, regions are exposed longer and to more direct radiation that is not spread out over a larger resolved area). These effects causes our seasons. |
 |
 |
Twice a year at special times (called the Equinoxes) the tilt is such that the length of the night and day are the same. Seasons, agriculture, and religious events are based around these facts. Calendars provide predictable information about when these events will occur. |
|
It takes approx 365¼ days (365.25 days) for the Earth to rotate around the Sun, and for hundreds of years this figure was used as the basis for our calendar. This calendar, called the Julian Calendar, was introduced by Julius Caesar in 46 BC. To accommodate the ¼ day partial, a leap-year was defined to occur every four years. In a leap-year an additional day is added to pick up the slack. We all learn about this in school. |
 |
 |
The reality, however, is that the true orbital period is a little less than 365.25 days. It's more accurately around 365.2425 days. This difference is small, only about 0.002%, but over centuries, this error compounds. |
|
The celebration of the festival of Easter is tied to the Equinox that occurs in the Spring, and the Roman Catholic church was upset about the gradual shift of this ceremony in the calendar. In 1582, Pope Gregory XIII made a couple of changes to address this issue. The first was to skip forward 10 days to re-align the calendar with the solar equinox, and the second was define a system to stop this happening again. (It's also at this point in history that the beginning of year was defined as being January 1st, instead of March 25th; Lady's Day. Interestingly, it is this reason that the tax system in the UK starts on April 6th, which is the lost days adjustment from the old Julian Calendar applied to the old start of the year!) |
 |
365.25 days, is 365 days 6 hours365.2425 days is 365 days, 5 hours, 49 minutes and 12 seconds.
To accommodate the time difference (365.25 - 365.2425 = 0.0075), in the Gregorian Calendar the frequency of leap years is reduced by removing three leap-years every 400 years (3/400 = 0.0075). This is done in a very elegant way: Leap-years still occur every four years, unless the year happens to be the turn of the century (every 100 years) when it is kept as a vanilla year. This additional rule, alone, would remove four leap years every 400 years, and we want to remove just three, so a final rule is applied that every four hundred years we make the century year a leap year after all (This last happened in 2000 AD which was a leap year despite being a multiple of 100). Pretty clever!
Though the Calendar is named after Pope Gregory, its design was proposed by a physician from Naples called Aloysius Lilius.
Even more stuff (warning your head might explode!)
NOTE 1: More accurate measurements still have determined that the tropical year is now know to be more precisely approx 365.24225. This could be compensated for by having 969 leap years in every 4,000 (instead of the 970 that the current Gregorian system would provide). It has been proposed that one leap year should be dropped once every 4,000 years. Nobody has agreed to this at the moment, and it's so far out that, sadly, I don't expect to be around when this issue arises.
NOTE 2: The Greek Orthodox Church, when it migrated from the Julian Calendar, adopted a slightly different Gregorian algorithm. Every four years there is a leap year, except when the year is divisible by 100 (so far so good), but here things change. The Greek Orthodox rule is to then divide the year by 900, and if the remainder is 200 or 600 then the year is a leap-year again. (So 1900, 2100, 2200, 2300, 2500, 2600, 2700, 2800 are non-leap years, and 2000, 2400 and 2900 are leap years).
This means that 218 in every 900 years are leap, so this system estimates a year at 365218/900 = 365.24222 days, which is definetly more accurate than the Gregorian approach [Good!] Sadly, however, the Greek Orthodox system will diverge from Gregorian in 2800 [Bad!] I'll warn everyone now, in the off-chance that my blog is still accessible eight centuries from now, with a glib "I told you so!"
NOTE 3: If you want to go deeper, pick up an Astronomy book and read about the difference between Tropical Years (or Solar years), and Sideral Years. The axis that our planet spins about wobbles (causing something called precession of the equinoxes), and so the point about which the day is the same length can be different from the position of where the planet would have been going all the way around. Don't worry, these differences are smaller still and with a frequency of around 26,000 years they are important to scientists, but nothing to worry about if all you care about is being late to catch a plane!
We could stop here
We've come a long way from Friday 13th, and now we know about the Gregorian Calender, we have all the background we need to prove the popularity of Friday 13th, but since we've dived so deep into celestial mechanics, indulge me in one last detour:
 |
Remember above that I mentioned that the Earth spins on its axis and it is this that causes our days and nights? Well there's a different kind of leap-correction that scientists sometimes need to apply. The Earth is spinning, and slowing down ever so slightly (no need to panic). Every now and then a leap-second has to be added to make sure things do not diverge. Atomic clocks are so accurate that these things are very important. Having a leap second is a blessing and a curse. It's good that our clocks are accurate enough to make sure that our days will not drift into each other, but it it's a curse to the IT industry. More and more of our lives are being lived online and stored and processed on computers. Goofing around with timing signals has the potential to play havoc with logs and code and transfers between systems. Documented problems have already occurred in computer systems because of the issue of needing to inserting an extra second. (Have you ever woken up and forgetten to update your clock because of a daylight savings time change? You can see the potential issues!) |
Since the leap-second correction system has been in operation, there have been a total of 26 leap second events. The most recent was June 30 2015. If you were around at midnight for this event and were standing in-front of a properly configured, leap-second aware clock, you would have seen a rare event. The seconds would have clicked up to 60!

A committee tries to ensure that the time difference between rotation time and our atomic clock time never exceeds an error of 0.9s, they have the power to do this by adding leap-seconds (or skip seconds if needed). Interestingly the change in angular velocity of the Earth is erratic (modified by tides, seismic and climatic events). Below is a graph of the delta over time. The vertical discontinuities represent when the leap-seconds were applied).
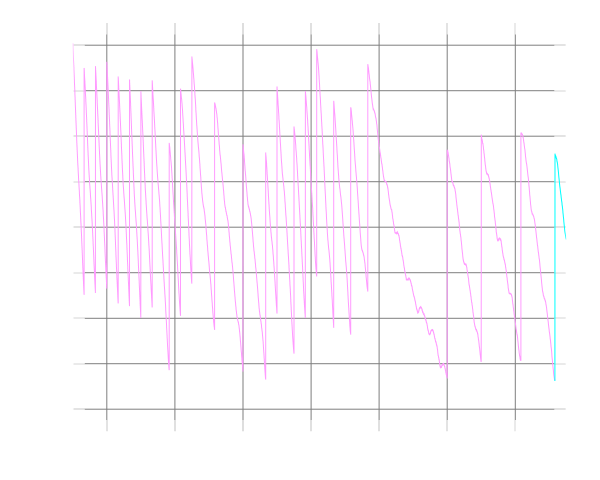
Note that when correcting, the committee waits for it to diverge to one extreme, then corrects to an opposite extreme, applying hysteresis, minimimzing the number of changes needed, and keeping the average error as low as possible.
Let me count the ways
 |
Now that we know all about the Gregorian Calendar, let's do some math: Each Gregorian 400 year cycle contains 146,097 days (You can calculate this from 365 x 400 = 146,000 for the vanilla years, plus an additional 97 days for the 97 leap years that occur). 146,097 is awesome because it divides by seven with no remainder (146,097 ÷ 7 = 20,871). This tells us that the pattern of days repeats every 400 year cycle. These days are spread over 4,800 months (400 years x 12). If we calculate the distribution over 400 years, since we know the cycle repeats, we know the expected distribution. |
|
The century non-leap years cause a disruption in what would be a revolving cycle of which day of week starts, and since January 1st, 2000 is a Saturday, it returns to this after 400 years without every day of the week having the same frequency of start. Remember, months don't have exactly 28 days, so this adjusts the thresholds. This is the distribution of the days of the week for days that are day 13: The difference is small, so I've offset the y-axis. (This is not cheating; when was the last time you you looked at a weather chart and the y-axis went down to absoloute zero! I'm just showing the difference.) |
 |
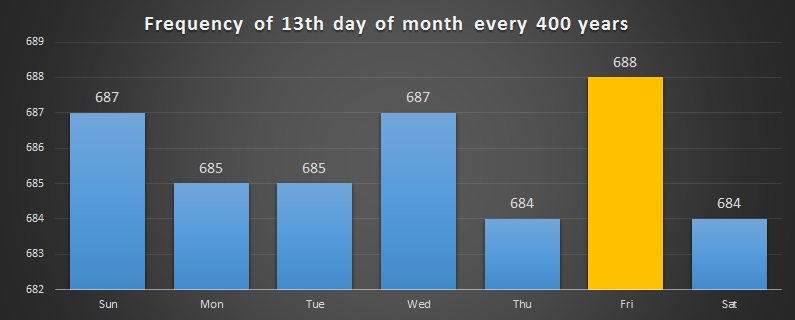
The modal day for 13th to occur on is Friday, with 688 occurrences in the 4,800 month cycle. (Of course, this is the same graph for the 6th as well as the 13th, 20th and 27th. Think about it!)
The least likely days to be the 13th are Thursday and Saturday.
Why?
 |
What's going on? Well in a vanilla year, there are 365 days. Modulo seven arithmetic leaves a remainder of one (meaning there is a remainder of 1 when 365 is divided by 7). This, ordinarily, causes a calendar to shift forward by one day each year (e.g. on non-leap years, if January 1st is a Sunday one year, it will fall on a Monday the following year. |
|
If there were no leap years at all, a calendar would cycle once every seven years (bad business for calendar printers, as people might be tempted to hold onto them!) However, every four years, we add an additional day, pushing the next year out two days. The congruence of these two facts combined causes our calendar (before Gregorian adjustments) to fully repeat after 28 years. If the story ended here, there would be no bias towards Friday 13th. |
 |
 |
In the Gregorian system, the year 2000 was a leap year, and then a 28 year rotation cycle of will pass, and another, and another, but after the third regular cycle rotation/sharing of days, we hit an irregularity at 2100 which is not a leap year. This causes the previous 12 calendars to repeat, and the pattern is not resumed until 12 years later (sort of like stretching that 28 year period over 40 years). The 40 year periods disrupt the distribution symmetry of days. January 1st, 2000 started on a Saturday, and this dictates the positions of all the other days, and when Friday's occur. The ratchet of the congruence means some days are more 'lucky' than others before the reset! |
Enough theory, show me a proof with real data
What is the longest period with Friday the 13th?
The longest period that can occur without a Friday the 13th is fourteen months.
This can occur either from July to September the following vanilla year (e.g. between 2001–02, 2012–13, and 2018–19), or from August to October the following leap year (e.g. between 1999–2000 or 2027–28).
Not so unlucky
|
There is nothing unlucky about the number 13, it's just a number. People don't suffer from bad luck, they suffer from a term described by psychologists as Selective Amnesia. What this means is that people only remembering events that correspond and reinforce their beliefs about luck. Conversely, their brains ignore or defocus events and outcomes that conflict with their philosophy. You can read more about this in my posting about The Gambler's Fallacy. |
 |