Coding is fun
Like all programmers, I get pleasure from writing code and solving problems. Sometimes I code just for fun. Today was one of those days. I thought I would share my results with you.
Padlocks with letters
 |
I was browsing the web and I came upon the image of an old padlock similar to the one on the left. It reminded me of a word puzzle I once read about that I had been meaning to solve, but never got around to. Some people have difficulty remembering numbers and, to them, a combination padlock using entirely numeric digits presents a challenge. These people might find more utility in a padlock whose combination is composed of letters so that a memorable word can be selected as the password. An example padlock using seven barrels is shown here. At first glance, it may appear that a combination lock using letters is much more secure than one using numbers because of the vastly increased number of combinations it affords. In theory this is true, and if the combination of the letter padlock is selected entirely at random then it produces a vastly expanding number of permutations. |
For a seven barrel example, a numeric only combination lock has 10 x 10 x 10 x 10 x 10 x 10 x 10 = 10,000,000 combinations. One using letters has 26 x 26 x 26 x 26 x 26 x 26 x 26 = 8,031,810,176 combinations.
In reality, however, a random combination is not used, and instead the tumblers are typically set to create a memorable word.
Using a very complete online dictionary, I was able to find just 23,109 distinct seven letter words in the English language. This represents a meagre 0.000288% of the addressable space. It's an illusion of security, and one that social-engineering hackers exploit. Sometime soon I'll write another posting on the (lack) of entropy in most passwords, but I'm getting futher and further away from today's puzzle …
The puzzle
|
Given a padlock (I believe the original problem stated it had five barrels, like the example here on the right), the puzzle was to find a pair of English words such that, when one the words was selected in the gate, the other word could be found somewhere on the barrel. For example, if the word FIZZY appeared in the lock gate, then a few letters around the barrel it would be possible to find the word KNEED. |

|

|
How would we go about solving this problem? Well, we could brute force all combinations of letters, check for a valid word and then see if this happens to generate any other words, but here I am using "could" in the politest way possible. Anybody who codes a solution this way should really not be coding! We need a much more elegant (and faster) solution. We can do much better … |
The process
Glancing at the padlock we see that the wheels are labeled in the same order. What this means is that, however the barrels are rotated, each adjacent barrel maintains the same relative (delta) between the pair of letters either side. What this means is that the two words (or more) in the solution to the puzzle must have the same relative spacing between their letters.
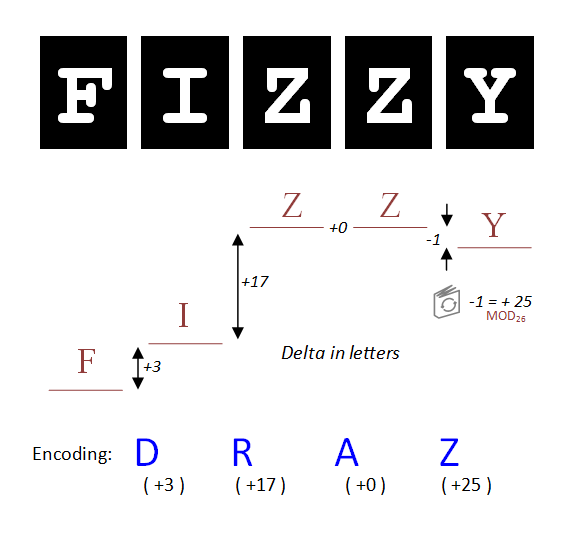
|
The diagram above shows this in pictures.
Staring with the letter "F" in FIZZY, we see that there is a delta of three letters to get to "I", then another seventeen letters to get to "Z". Since there are two letter "Z"s in a row, there is no delta, and finally to get from "Z" to the "Y" we need to step back one letter.
So now, we have an encoding for the word FIZZY, and it's +3, +17, 0, -1. (After the first letter, we go on 3 letters, then on 17, then repeat the same letter, and finally go back one). All words that appear on the barrel at the same time will have the same encoding. Computer guys like to call this a HASH FUNCTION, it's a repeatable encoding/index system.
Time for a bit of house keeping. Negative numbers can be a bother to work with, and also since there are only 26 letters in the alphabetic, if we're looking for, for instance, the letter that is +17 past the letter "T", we're going to shoot past the end!
Thankfully, both these issues can be solved by the use of Modulo-26 counting. This is analogous to the odometers of days of old. We just wrap around. If a letter goes off the end, past "Z", we simply subtract 26 and start again at the letter "A". In this way, subtracting one from a letter is really just the same as adding twenty five (going around the clock as needed).
Encoding
One more step to go, then we have everything lined up. It is possible to work with the number chain +3, +17, 0, -1 to search for candidate words but it complicates things to have to work with more than one value (meaning it's not elegant coding).
Those blessed with some math experienced will realize that we could encode this HASH value into a single numeric field using base-26 numbers. This is a very elegant solution, and in any interview I'd give you top marks for proposing that solution.
|
What I elected to do is use letters to represent my number base (can you can see it's the same thing?) In my encoding, A=0, B=1, C=2 … Z=25. (It really does not matter what encoding you use as long as it is repeatable). So for the word FIZZY, the encoding is DRAZ. All words that appear on the tumbler at the same time as FIZZY have the encoding of DRAZ. Ok, we've just turned onto finals. We download a database of words from the web, store it in our favourite database tool (I use Microsoft SQL Server), add a column for the encoding and pre-compute all the deltas values. |
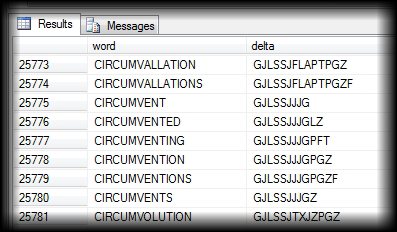 |
Now it's a simple query (fast) query to find the all rows with duplicate encoded values. "Done!"
Results
I used a database containing approximately 170k English words. Below are the results.
Seven Letter Soutions
I found two seven barrel solutions:
SULPHUR with PRIMERO
NOWHERE with ABJURER
Six Letter Soutions
There are eleven six barrel solutions:
TUFFET with STEEDS
INKIER with PURPLY
MUUMUU with WEEWEE
GRUNGY with ALOHAS
BOUFFE with ANTEED
HUSHED with BOMBYX
MANFUL with THUMBS
PEPPER with LALLAN
FUSION with LAYOUT
KERNEL with GANJAH
DAWTED with SPLITS
Five Letter Soutions
There are 93 five barrel solutions:
|
HINTS and STYED DELED and STATS STEER and TUFFS TUMMY and NOGGS NONET and UVULA MOTTE and GINNY MOCHA and SUING SURGY and MOLAS ADDER and BEEFS FILLS and LORRY LOTTE and FINNY BENNI and RUDDY KNEED and FIZZY GLARY and PUJAH PULPY and VARVE PUNTY and JOHNS INGOT and CHAIN DIDOS and PUPAE CHEER and JOLLY HOTEL and OVALS GNARR and AHULL GNARL and XERIC NULLS and TARRY TASSE and HOGGS |
HOLLY and BIFFS TAZZE and NUTTY MUFFS and SALLY SARIN and MULCH MULES and SARKY SASSY and MUMMS MUNCH and SATIN GOLLY and MURRE GOLEM and MURKS LUFFS and RALLY RALPH and OXIME RAPHE and CLASP RATAN and VEXER VEALY and OXTER LUTEA and PYXIE TELOI and WHORL TENET and ALULA GREEN and TERRA DOLLS and WHEEL EPOCH and ALKYD CORKY and WILES WIVER and FRENA FRERE and SERER |
COGON and SEWED SECCO and COMMY BOURG and VIOLA BOLLS and HURRY MARRY and GULLS GULPS and MARVY OCTAD and DRIPS GULFS and MARLY MASSE and GUMMY GUNNY and MATTE APTLY and TIMER CRAAL and PENNY PERRY and CREEL CREDO and SHUTE LATTE and FUNNY LATER and SHALY LATEX and SHALE TIFFS and SHEER TIGER and PECAN RIVER and ARENA CUBED and MELON CURLY and WOLFS WOMBS and CUSHY |
BUFFI and HALLO HARRY and BULLS BUNNY and SLEEP BUTYL and HAZER GANJA and KERNE GASSY and SMEEK FADGE and TORUS TOUCH and FAGOT JERKY and SNATH SNEER and TOFFS SORRY and MILLS LINUM and ROTAS HERMS and DANIO EBONY and UREDO DATED and SPITS SPOTS and DAZED ECHES and KINKY JIMMY and POSSE JINNS and POTTY POTTO and JINNI BAIZA and TSARS BANJO and FERNS SETAL and AMBIT |
Four Letter Soutions
There are 331 four barrel solutions, including 15 where there are triple words on the barrel.
|
DEED and ABBA and NOON BEEF and LOOP and PSST PYIC and RAKE and FOYS PAPA and JUJU and DODO NAAN and ANNA and BOOB ASCI and SKUA and MEOU EAUX and OKEH and SOIL DADO and AXAL and HEHS |
PREX and YANG and WYLE GLIB and JOLE and ZEBU YETI and FLAP and SYNC LANE and SHUL and PERI PERK and SHUN and LANG FUJI and APED and PETS BYRE and KHAN and SPIV |
|
DEER and EFFS STUN and DEFY ABET and HILA HINT and STYE TUBE and HIPS TUBS and STAR STAT and DELE STEP and OPAL OPEN and STIR TUNG and GHAT HIDE and STOP TUSK and NOME GIMP and CEIL MOTT and YAFF ACHE and GINK GIRD and PRAM PRAU and GIRL CEPE and MOZO YANK and CERO MODI and WYNS SULK and ACTS EGAD and MOIL SUPE and GIDS MOLT and PROW PROA and SURD SURE and MOLY SURF and GIFT MOLA and PROD PROG and MOLD GIGA and YAYS CEDE and MONO MONS and CEDI ORRA and BEEN BEER and ILLY BEET and ADDS FILS and LORY KNUR and RUBY RUCK and LOWE RUDE and FIRS TWIN and LOAF ORDO and TWIT RUGS and LOAM KNAP and BERG KNAR and LOBS LOCH and RUIN KNEE and FIZZ FIBS and RUNE RUNG and ILEX FIDO and KNIT FIGS and RUSE LONE and BEDU KORS and WADE WAGE and QUAY QUEY and WAKE WAME and KOAS KOBS and WANE WAST and SWOP DIVA and VANS JOBS and VANE VANG and ZERK TYNE and PUJA PUKE and JOEY PULL and TYPP VARY and PULS |
TYPY and VARA TYPE and PULA VASE and JOGS JOHN and PUNT PUNA and TYRE DIBS and CHAR CHAT and PUNG PUNK and TYRO VATS and GLED DIDO and PUPA DIES and JOKY CHEF and PURS JOLT and INKS GLIA and CHEW IONS and DJIN AHOY and TAHR TAKE and HOYS BITT and TALL TALK and BITS HOBS and GNAR GNAT and TANG TAPE and HODS HOGG and TASS NUMB and ELDS BIAS and TASK AHEM and HOLT HOMY and BIGS GOOD and WEET WEED and GOON GORY and AILS SAIN and MUCH OWES and GOWK GOYS and SAKE SALL and MUFF SALP and WEPT SAMP and GOAD GOAS and SAME GOBO and WERE GOBS and SANE SANK and GOBY SARK and MULE MUMM and SASS MUMU and GOGO EMIT and WEAL WEAR and SAWN LUVS and ENOL CLOY and FORB CLOD and RADS RAGA and LUAU LUBE and ZIPS RAIL and ENVY FOXY and LUDE UDOS and OXIM FOZY and ZITS FOAM and LUGS RAPS and CLAD CLAP and RAPE RASE and FOGS FOHN and LUNT LUNY and RATE LUNA and PYRE FOLK and IRON FONS and RAZE LUTZ and FONT |
QATS and BLED ALLS and TEEL DOPY and WHIR WHIT and DOPA GRUB and DORY TEMP and PAIL PAID and ALTO DOXY and GRAB ITCH and TENS DOFF and PARR PASE and DOGS ALES and PATH PAWN and TEAR DOLL and WHEE DOLS and JURY GROW and DOLT JURA and WHEN WHEW and GROG COON and SEED CORD and FRUG CORE and WILY WILE and CORK COTE and WINY UGLY and OAFS SEMI and COWS FRAG and SENT COZY and WITS COBB and FREE SERA and WIVE MYNA and AMBO COIN and WICH AMIA and SEAS COLT and FROW FROG and COLD ERRS and REEF BOON and REED NABE and BOPS BOUT and ANTS HUFF and REPP NAME and BOAS NANS and VIVA NAOI and HUIC BODS and NAPE BOFF and HULL HUNH and ANGA ANIL and NAVY REAR and ERNE BOMB and HUSH VIGA and NAYS REDO and BONY DRAB and GUDE GUFF and MALL MAMA and ESES GULS and DRIP DRIB and MARK MARL and GULF ESPY and THEN MAZY and GUTS PEED and ZOON ODES and ETUI FUZE and TINS SHOW and PELT SHOG and ETAS TIPI and PELE |
PENS and ETCH CRAG and PENT CRAP and FUDS PEPS and ODOR PEPO and TITS FUGU and LAMA CRIB and LARK LASE and FUMY PEAN and TIER PEAR and LAWN FURS and CROP CROC and SHES PEDS and APOD BRUT and SILK SIMS and AQUA KAES and SIMA SIRE and BRAN KANE and YOBS BRIN and SIZE BRIE and KARN IZAR and JABS HYMN and NEST HYPS and ARIL DULY and NEVI RIBS and DUNE DUPE and RIDS RIFF and DURR DURE and RIFS MEET and WOOD UMPS and GYBE PHEW and WOLD WOLF and CURL CUSS and OGEE SLOP and HADE PILY and SLOB PILE and IBEX HAES and PIMA PINT and OHMS PINY and VOTE PIPE and ATAP HAJI and SLUT HALL and BUFF ATES and PITH PIXY and SLAB SLAG and UNCI UNCO and SLAM LEVO and HARK EXON and BULK ATMA and HATH HATS and SLED PIER and LEAN HAWK and PIES SLIP and BURY BUTS and HAZY EYAS and SMOG GAEN and KEIR KEPI and GALE JEED and TOON SNOW and IDEM TOPH and SNOG TORR and NILL TORS and FADE TORY and NILS TORC and FADO |
JEHU and TORE TOUT and DYED TOYO and NISI TOYS and FAKE FANG and JERK FAUX and TOIL NIDI and FAVA FAZE and TONS MILT and PLOW PLOY and SORB PLED and EATS ROOD and OLLA ROOF and EBBS CZAR and DABS HEIL and LIMP LIMY and ROSE LINN and DAFF LINY and ROTE SPUN and LING LINK and SPUR ROUT and LION LIPS and HELO HELP and DAHL DALE and SPAT SPAZ and LITS ROAD and DAMP HERN and UREA HERO and DANK URGE and SPEC SPED and HETS DASH and OLDS LIAR and HEWN KHAF and SPIN SPIT and DATE SPIC and BYRL BYTE and LIDO LIES and DAWK DAWN and HEAR DAZE and SPOT ECHE and KINK KITS and CALK CANS and KIVA CANT and TREK CAPS and ECRU CAPO and GETS CARP and TRIG BAAL and EDDO FEET and POOD POON and FEED BABE and POPS BAFF and JINN JISM and BAKE BALK and ONYX AZON and FETS BARB and SRIS ONES and BARF BASK and POGY BATT and JIBB JIFF and POLL |
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.