Steganography
Steganography is the art and science of hiding messages in a covert way such that, unless you are party to the decoding secret, you are unable to detect or decode.
An advantage to steganography over simple cryptography is that, if done well, viewers are entirely oblivious to any changes. Even those party to the secret should, ideally, not be able to detect anything suspicious.
I've seen people talk about hiding hidden text messages in images but, for fun, I wanted to experiment with hiding other images inside images. This blog posting contains some of my results.
Can you detect any hidden image in the Chicago Skyline below? Do you see the aircraft? No, then read on …

Theory
A typical computer image these days uses 24 bits to represent the color of each pixel. Eight bits are used to store the intensity of the red part of a pixel (00000000 through 11111111), giving 256 distinct values. Eight bits are used to store the green component, and eight bits are used to store the blue component.
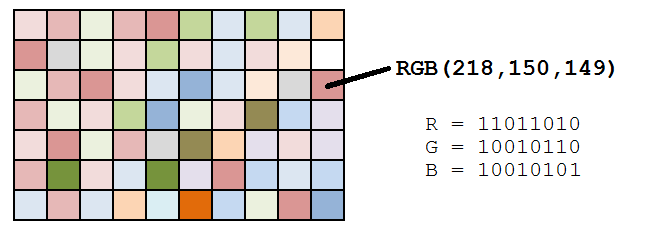 |
The diagram on the left shows how each pixel of an image can be described by three 8-bit binary numbers. |
Whilst it's great to have a wide dynamic range of colors, the human eye does a poor job of distinguishing subtle differences between two very similar shades of color.
 |
Take, for example, the orange colored bar here on the left. The left half of the bar is shaded RGB (255,127,39) and the the right half is shaded RGB (255,126,39). A subtle change to the green value by just one unit. Can you detect it? |
Exploiting this fact allows us to encapsulate information into the image. Because our eyes are not able to detect the difference between two adjacent color values, we can write code to manipulate this last binary digit (called the Least Significant Bit in computer lingo because a toggling of this value makes the smallest change to the the value of the number) for our nefraious benefit.
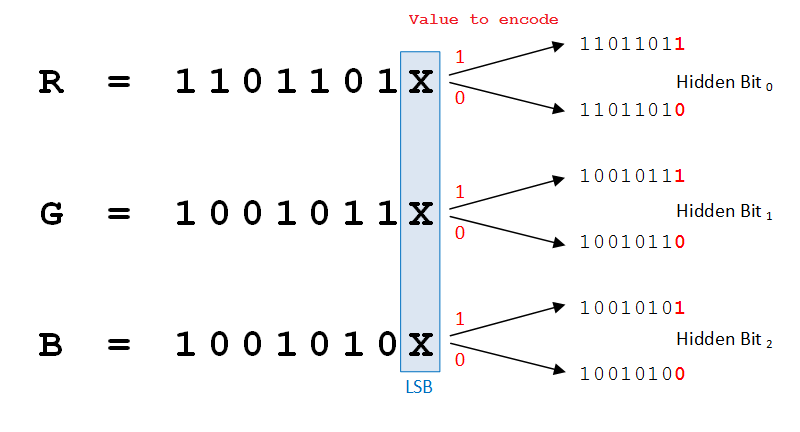
If we want to store a hidden bit value of one, we simple make sure that the LSB of the byte we are interested in is set to one. Similarly, if we want to encapsulate a hidden bit value of zero we make sure the LSB is zero. This is very easy to do with some boolean bit manipulation. At most a color value will change by one unit and, as we have seen from the orange bar above, we don't really care what the original value was.
Because there are three color channels (Red, Green, Blue), it's possible to store three hidden bits of information in each pixel.
Three hidden bits allows each pixel to store a value of between 000 – 111 (decimal 0-7). Enough for an eight-grey shaded image.
Note - There is a 50:50 chance that the LSB is already the value we need, and so no change needs to be made to that color channel. Because of the vector nature of colors, even if every bit in our source image needed to be changed, the change will still be very miniscule. Geek Note - I did try the experiment of storing just one bit of hidden data (enough for a Black & White image), by toggling the LSB of just one random color channel (and using parity to encode the hidden bit) in an effort to minimize the error of each colored pixel. However, as we will see later, it's surprising just how far it's possible to pull colors before the eye notices, so I dropped that algorithm in favor of the three-bit one. |
 |
Results
Remember the city skyline image at the top of this post? (scroll back up and take a look). That image already contains the gray-scale image show below (encoded using the three bit algorithm).

To show you just how subtle the change is, here is a composite image I've constructed using the Source image, Hidden image and Cypher image. The right half of the image below is the original (un-modified) picture. The left hald of the image is the encoded composite cypher image. It's not possible to even detect the joint! The bubble shows a cut-away revealing the hidden image. Even though you can trace the lines on the aircraft out to where you know they go, your eyes can't detect the encoding of the subtle single digit change in pixel values.

Limitations
There are many limitations to this particular algorithm/implementaton. It relies on every single bit of information in the image being preserved. If, at any stage, the image is converted to a lossy format for storage (such as JPEG file), the subtle color information is lost. Even simple rounding/changes, smoothing, color palette optimisations, contrast adjustments; totally blows away all the hidden information, and you only get garbage noise when decoding.
Mitigations
Having a little extra spare time, I did some experiments about ways to make the cypher image less sensitive to recoloring and color adjustments. I did this by trading off color range in the source image against color range for the hidden image. Our current algorithm used 7 of the 8 possible bits (per color) to represent the source image, and only one bit to encode the hidden image.
This is easy to change. What are the consquences of of using less bits for the source image, reserving more for the hidden image? The negative impact is that we lose granularity in the color of the source images; the colors get quantized into ever more widely spaced buckets as the number of bits is reduced. Our original implementation allowed each color channel to contain one of 128 possible values (down from 256 when all 8 bits were used). Adjusting the algorithm to a 6:2 split from 7:1 means there are now only 64 discrete values each color can be, and moving to 5:3 reduces this to just 32. So why do it?
With the extra bits in the hidden domain, we can do one of two things: We can either increase the color depth we can use for the hidden image (allowing more colors/grays to be used), or, we can keep the same color depth and have some robustness in the palette. Experimenting with the later, and keeping to my orignal 3-bit encoding, I found that it possible to keep the hidden image preserved even if the contrast or brightness of the cypher image is increased and decreased; The result of using more bits for the hidden image is that there is now a continuous range of values that represent a particular bit on the hidden text, so minor changes to the color values of a pixel still keep the color in the range required to decode a correct value.
Examples of adjusting the bit split
Here are some examples of the effect to the cypher image by moving the balance between the number of bits to encode the hidden image and the number of bits to encode the source image.
Below are three images. The balloon image on the left is the source image. It's in 24-bit color. The image in the middle is an gray-scaled self portrait. It's already been thresholded to use 3 bits (8 gray levels). The image on the right is gray-scale color bar.
 |
 |
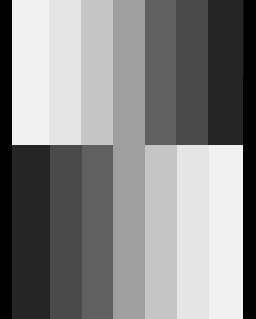 |
| Source | Example 1 | Example 2 |
Results
The images below all contain hidden images. Those on the left contain Example 1 and those on the right contain Example 2.
 |
 |
This is the orginal algorithm using seven bits to represent the source and reserving just one bit per color channel for the hidden image. Both examples look very close to the original source. It's not possible for the eye to determine any difference. |
 |
 |
These two images show the result of reducing the number of source color bits down to six. We've halved the number of distinct number of colors again, but still its not possible to tell the difference, even when we know to look. |
 |
 |
We're now at 5 bits of color for the source image (just 32 distinct levels per color channel), and if you know what to look at, and have a good monitor, you might start to see contours in the colors, but still, it's hard to tell. |
 |
 |
Now we're at 4 bits of color for both the source and hidden. The cypher images are noticeable degraded in quality. |
 |
 |
Yugh, things are starting to look a little ugly! |
 |
 |
We can now see the hidden image starting to bleed through. It's harder to make out the face on the left image because of the ditherting, but the vertical lines from the color bars on the right are stong. |
 |
 |
Here there are just a couple of colors used in the entire image. Even if this image were brightened or darkened a considerable amount, the colors would not change significantly enough to not allow 100% decoding without error. |
Need more convincing?
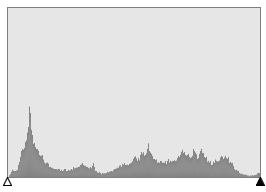
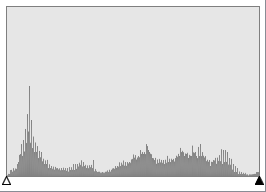
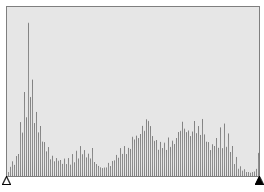
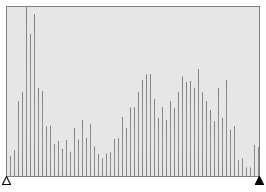
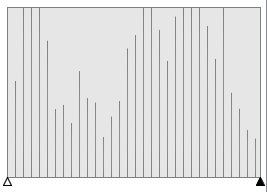
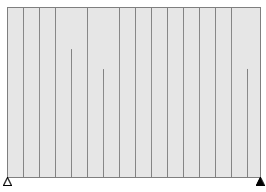
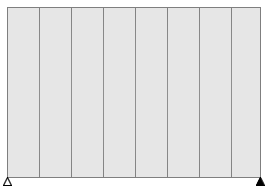
I have to admit, I was sceptical when I saw the top few results. It's hard to imagine just how insenstive our eyes are to loss of bit-depth of color. At first I thought there was error in the code! To prove otherwise, I loaded up the images in a paint package and plotted histograms of the colour distributions (in this case the red channel). Here are the results (source image at the top, and decreasing bit-depth as you go down).
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
You can clearly see as the number of bits used to represent the colors decreases, the quantizement increases.
Geek Note
In generating the bit-split, it's not as simple as masking off the top n–bits and using these for the source image and the rest for the hidden image because this would defeat the purpose of this exercise (making the image robust to minor changes in color that might occor). This is because of the way binary numbers work.
 |
Imagine, for instance if one of the red pixels had a value 119, we'd want this pixel to be sensitive to a minor change in value (to take into account some image brightening or releveling) so, for instance +/- one unit should not cause the encoded value to change. |
However, if we look at the binary representation of numbers 118, 119 and 120 we can see that a change of just one unit of color can make a huge difference to the binary representation of the number. If we'd encoded the hidden image simply using the lowest three bits of the color number, a one unit change to the read color value would make a huge change to the encypted value; foiling the purpose of making the implementation damage tollerant.
Instead of simply masking the bits to encode the hidden image bits, I used a modified lookup table in which each candidate value is read and then snapped to the nearest of the quantised values for the color in that bit-depth based on the number to encode. (i.e. selecting the new color with which has the lowest absolute error from the color in the source image based on the value required). Based on the color depth, the bit to be encoded is striped 1 or 0 to minimize total error of colors moved for the whole image.
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.