
	Advertisement

Bertrand's Box

Imagine there are three identical treasure chests in front of you:

The first box contains two gold coins.

The second box contains two silver coins.

The third box contains one gold coin and one silver coin.

Random draw from a random box

The boxes are shuffled so that you don’t know which is which. You select a random box and, without looking inside, reach in and pull out one of the coins at random. You close the lid after selection, then look at the coin you picked. It is a gold coin.

Question What is the probability that the other coin in the box is also gold?

Symmetry?

Without thinking about it too closely, your first answer might be ¹/₂ (because of symmetry of the system and the fact there are the same number of gold and silver coins.

The actual answer, however, is ²/₃ and this, confusing to many, answer is given the name Bertrand’s Paradox after the first person to publish it, a French mathematician called Joseph Bertrand (1822–1900) in his 1889 text Calcul des Probabitités.

To easily see why the answer is ²/₃ we need to enumerate all the possible combinations of ways the coins can be arranged:

Here you can see where the issue lies because the box that contains the both gold coins will always allow you to select the gold coin (and there are two ways this could happen).

Out of all six (equally likely) ways that the coins can be arranged we can see that, in two of the three cases when a gold coin is selected, the other coin is also gold. Therefore the probability that the other coin is gold is ²/₃.

(Another way to think of this is that there is no way the coin could have come from the box with the two silver coins, and so the gold coin must have come from the mixed box, or the totally gold box. Of the four solutions, one is not possible, and the other three are equally likely. Two of these three solutions has the other coin gold).

There is symmetry in the system because, for a chosen box, it has two coins that are the same ²/₃ of the time. So, regardless of what kind of coin is chosen, the box has two coins of that type ²/₃ of the time. In other words, the problem is equivalent to asking the question:

“What is the probability that I will pick a box with two coins of the same color?”

Other variants

I’ve seen this puzzle discussed in other variants. A common one is with three cards:

A card that is black on both sides.

A card that is white on both sides.

A card that is black on one side, and white on the other.

All the cards are placed into a hat and one is pulled at random and placed flat on a table. The side facing up is black. What are the odds that the other side is also black?

Studies show that, when the question is posed this way, a majority of people get the answer incorrect.

However, if you pull out a random card and phrase the question as “What are the odds that the color on the other side of this card is the same?” (essentially the same question), many more people get the question correct.

It seems it is much easier for people think that, as only one card of the three is mixed, and two cards have matching backs, there is a two in three chance the back of the card matches!

It’s all how you phrase the question!

Bonus Puzzle

Imagine that you created labels for each of the boxes to accurately describe their contents.

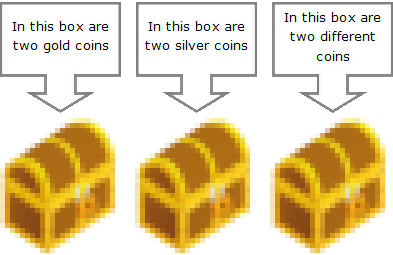
Then, overnight, some mischievous pixies fly in and mix up your labels. These playful little pests cunningly rearranged all the labels so that no label is now correct!

Question What is the minimum number of coins you’d need to select, and from which of the boxes should you do it, to be able to correctly re-label each box?

What strategy should you employ?

(Think about it for a second before reading the answer)

Interestingly, you can solve this riddle with just one sample. Here’s what you do:

Go to the box labelled “both” and select one coin. (Let’s say it’s silver coin). Since we know that label “both” is in the wrong place, this must mean that this box must be the entirely silver box. We can switch the label of this box to silver. This fixes one of the boxes, and, as know the other two labels are bogus, all we need to do is switch the other two. Problem solved!

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.