
	Advertisment

Consequences of a living on a sphere

We all (now) know that the World is curved. At kindergarten we’re told the Earth is like a ball.

At high-school we’re told it’s a called a sphere.

At college we learn it’s an oblate-spheroid. (After millions of years of spinning, it’s a little fatter around the equator than it is going around over the Poles). The difference is small, but very measurable.

If you go on to study further, you’ll drown in the mathematics of Spherical Harmonics. I’m not going to delve into that today. (I've been there, unless math is your passion, you might want to play elsewhere. I have no interest in returning!).

Today, we’re going to go back to a kindergarten model and assume the Earth is a round ball. We're going to look at a couple of consequences of that. First off, how far can you see?

How far is the Horizon?

Because the World is not flat, you can’t see forever. As you look out to the horizon the planet falls away from you. This limits what you can see. Just how fast does this happen? How far can you see? Let’s break out a little math to find out.

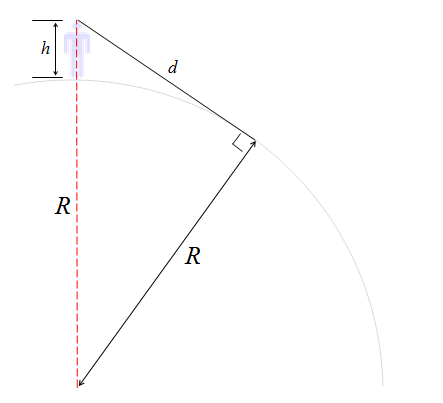If we stick with assumption that the Earth is a sphere (and a smooth and uniform one at that), we can produce a diagram like the one on the left.

A man of height h stands on a sphere of radius R and looks out to the horizon. The furthest point he can see is defined by the tangent that grazes the Earth and passes through his eye.

By definition, a tangent is normal (perpendicular) to the radius and so we can create a right-angle triangle with a hypotenuse of length (R+h). For the two sides of the right-angle, one will be of length R, and the other will be the distance the man can see (which we’ll label as d).

Using Pythagroras, we can creation an equation showing the relationship between all three sides of the triangle.

Expanding, then simplifying, allows us to compute an equation giving the distance to the horizon based on the radius of the the planet and the height of the viewer.

Note – Of the two terms under the square root, the left term dwarfs the right term. I'll keep it in there, but as we run through some calculations you'll see that, until we reach a viewing altitude of something like a spacecraft in orbit, it can be ignored.

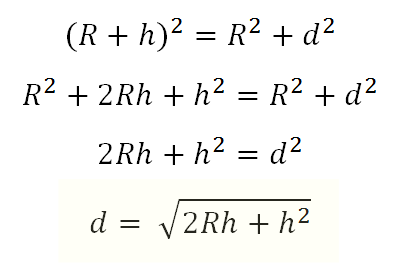A Person

An adult person of around 6 ft tall has eyes approximately 1.8 m above the ground (yes, I'm using the Metric system). For the radius of the Earth, I'm going to use the value 6,371 Km (the mean radius).

Plugging in these values …

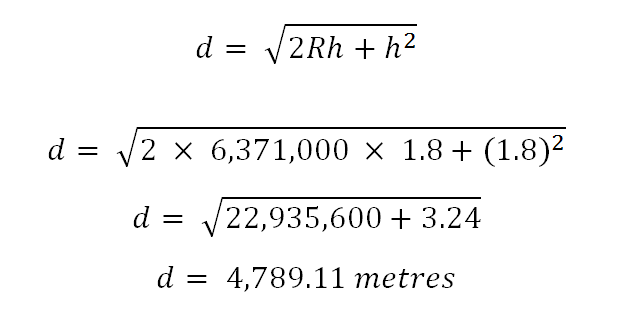
(We can see here, as commented above, that the right little term is dwarfed by the left term involving the radius).

The solution is that the furthest an adult can see is 4.79 Km (which is just short of 3 miles).

A child

A little child is closer to the ground. An average four year old is around 1 m tall. A child at this height can see just 3.57 Km (Eight tenths of a mile less than an adult).

Tip – Put your child on your shoulders, and when they are sitting there, they should be able to spot things on the horizon around half a mile before you! (This is useful to know when dragons are chasing you).

Taller viewpoints

What if we're higher up?

The top observation deck of the Eiffel Tower is at 273 m.

From this altitude, the horizon will be 58.98 Km away (36.65 miles).

The top floor of the Burj Khalifa tower in Dubai is 621 m high.

This would give a viewer a theortical view over the desert of 88.96 Km (55.28 miles).

Is it bird? …

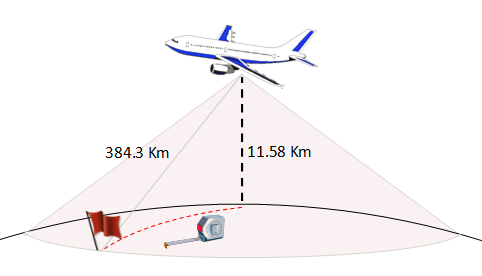
An airliner cruising at 38,000 ft is at an altitude of 11.58 Km

Plugging this into the formula reveals an answer of 384.3 Km, which is 238.8 miles.

NOTE – The distance to the horizon we caclulate with our derived forumla is the straight line distance from the viewer to the ground (the edges of the cone in the diagram to the left). How different is this to the distance that would be measured if we started directly under the plane, and pulled a tape measure around globe to the point where the tangent scrapes the surface?

When we were dealing with small altitudes, the difference between the straight line distance, and the ground distance along the curve of a planet was insignificant.

Let's calculate the delta between these two distances for our cruising aircraft.

To do this, we'll use a little trigonometry. Below is a diagram showing the subtended angle (from the center of the Earth) and it's relationship to the distance to the horizon.

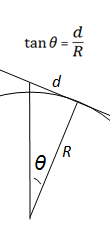We know the circumferance of the Earth, it's 2πR

If we know the subtended angle, we can determine what ratio this represents of a full circle, and thus what ratio of the circumference this represents. This will give us the distance along the ground betweeen the two points.

Using the values of d=384.3 Km and R=6,371 Km, and using the tan^-1 button on our calculator we can calculate the subtended angle. It's 3.452°

(3.452/360) x (2 x π x 6371) = 383.8 Km

For a plane at high altitude, the difference between the straight line distance to the horizon and the curved distance on the Earth is about 500 m. (The difference when dealing with our first example of a man of height 1.8 m is a fraction of a millimeter).

This segues nicely into our next example, the Golden Gate Bridge.

The Golden Gate Bridge

The Golden Gate Bridge, possibly the most photographed bridge in the World, spans the opening of San Francisco Bay. Completed in 1937, it boasts two towers of height 230 m and these are 1,280 m apart.

Trivia - Want to paint your house the same color as the Golden Gate Bridge? Here are the CMYK colors: C= Cyan: 0%, M =Magenta: 69%, Y =Yellow: 100%, K = Black: 6%.

Because of the curvature of the Earth, the towers are a little wider apart at the top than at the bottom (see exagerate diagram below). Let's calculate how big this difference is.

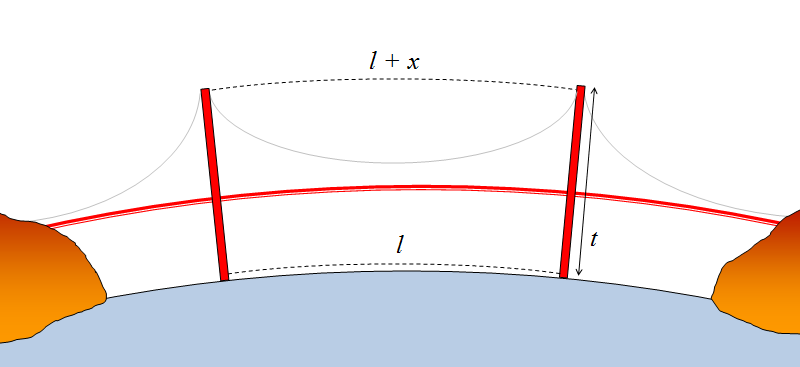
We're assuming the towers are constructed perpendicular to the ground. We'll use l to represent the distance between the two towers at their base (1,280 m), and t to represent the height of the towers above the ground (230 m). We'll use x to describe the difference between the towers at their tops.

Similar to above, we'll calculate a ratio using the subtended angle. There are two similar segments, one with arc length l and a radius of R, and one with an arc length of l+x and a radius of R+t. Both of these segments share the same subtended angle on the globe.

The top equation on the right shows the ratio of the lengths of the arcs to their respective circumferences.

A few lines later, and we have a simple formula for the difference between the two arcs.

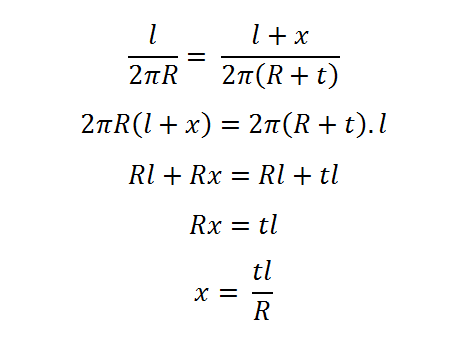Plugging the values in reveals that x = 46.2 mm (that's about 1¹³/₁₆").

The top of the Golden Gate Bridge is almost two inches wider at the top than the base because of the curvature of the Earth!

Tell everyone in the car this next time you drive over it!

Refraction

Before my inbox gets flooded with comments, yes, it's true, my horizon calculations were very simple and I assumed no complications with the refraction in the atmosphere. In real life, our atmosphere is a very complex and dynamic organism filled with a mixture of gasses and vapors. It has pressure gradients, winds, temperature gradients and refracive index differences. Much of these variances act in your favor, and on most days, because of refraction (the bending of light between media of different densities), the distance you can see to the horizon is greater than simply geometery calculates.

You can find a complete list of all the articles here. Click here to receive email alerts on new articles.