Cylinders in Spheres
What is the largest cylinder that is possible to fit inside a sphere? Let me make that a little clearer. Out of all the cylinders that it is possible to carve out of a solid sphere, which one has the highest volume? Or, as an even better definition: What is the highest achievable ratio of the volume of the cylinder to the volume of the donor sphere?

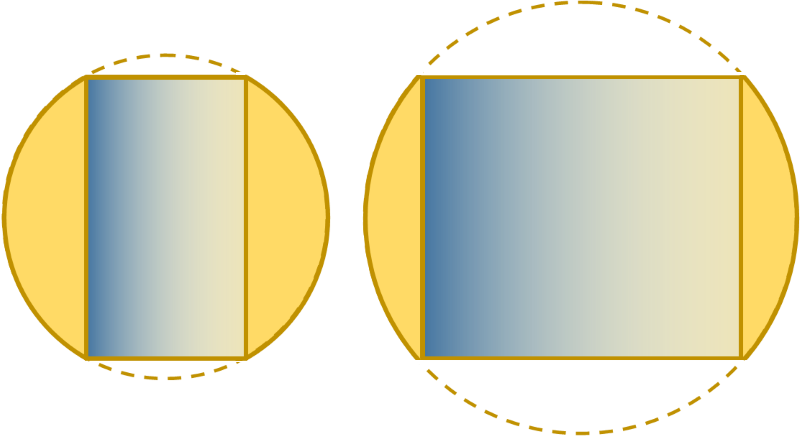
Obviously, if it’s going to be the highest, it’s going to have to touch the edge of the sphere, and from symmetry you can appreciate that it will take the form above (where the entire circular edge of each cylinder end-cap touches the sphere), but is the optimal solution a fat squat disk? Is it tall thin cylinder? Or is it somewhere in-between?
Geometry Time
Let's start with a few definitions:
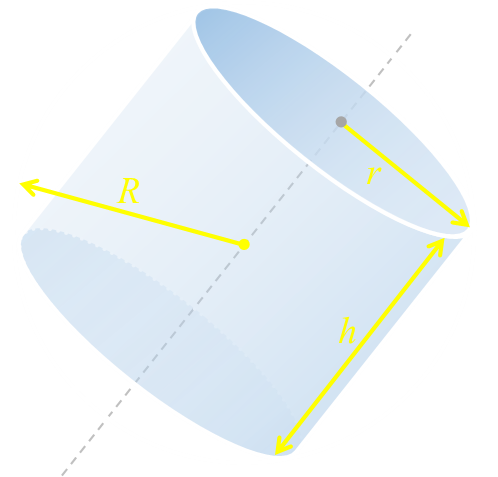 |
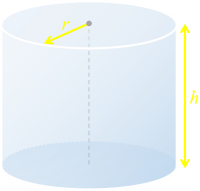
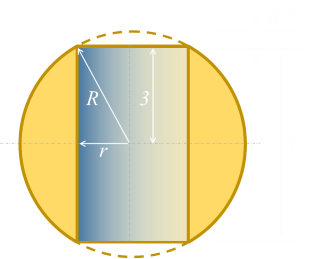
R The radius of the sphere h The height of the cylinder r The radius of the cylinder
Vc The volume cylinder Vs The volume sphere |
|
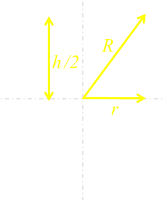
Imagining a cross-section through the center of the cylinder we can see the following geometry. The radius of the sphere defines the hypotenuse of a right angle triangle, and using simple Pythagoras we can define the relationship between our variables: 
|
|
|
The volume of a cylinder is the area of the circular cap multiplied by its vertical height: 
The volume of the sphere is defined by this standard formula: 
|
Calculus
It's time to wake up Newton and Leibniz. We're going to break out some high school calculus to solve this problem. Here is the equation for the volume of the cylinder, and into it I've substituted the cylinder radius with that derived from the Pythagorean geometry.
We have our equation for the volume of the cylinder, now we'll take the first differential with respect to height:
If we set the first differential to zero, we can find the turning points in the function.
 |
A quick confirmation confirms that the second differential is negative (meaning that the turning point is a maximum value). This gives us our first first result: the value for the height of the cylinder when the it has maximum volume. |
Substituting back in
Now that we have the value of h for maximum volume, we can substitute this back into the equation for the volume of the cyliner Vc
Result! We have the formula for the volume of the maximum cylinder that can be carved out of a sphere.
All that is left to do is normalize this by dividing it the volume of the sphere. The final result is the ration of the volume of the cylinder to the volume of the sphere. This is a very pleasing result.
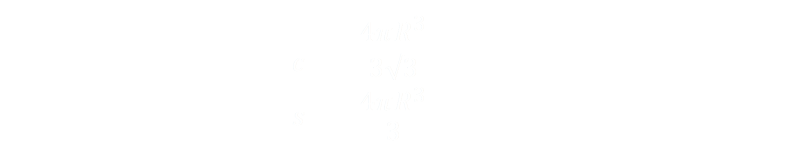
Graph
We'll pause here for a second to plot a graph. It's interesting to look at how the volume of the largest possible cylinder changes with respect to the height of the cylinder.
On the x-axis, I've plotted height h ranging from zero on the left (an infinitesimally thin disk with the same radius as the sphere), to 2R on the right (a stick from pole-pole with no cross-sectional area).
On the y-axis I've plotted the ratio of the volume of the cylinder to to the volume of the sphere.
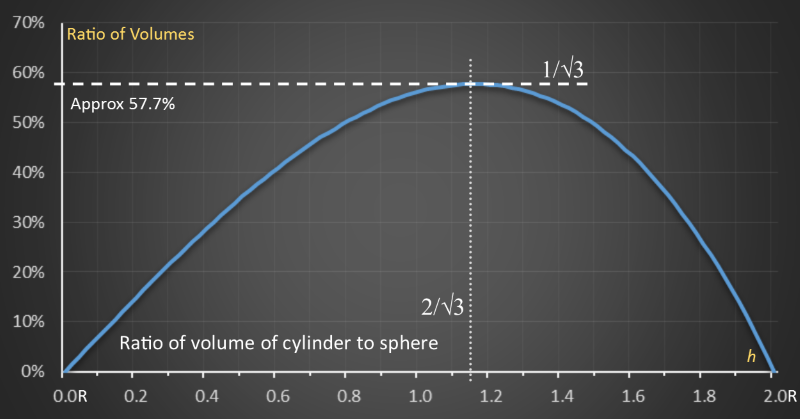
The curve clearly shows the maximum point at the calculated value, and falling off to zero at the two extremes.
Further down the rabbit hole …
 |
At either end of the cylindrical plug are two spherical caps. These are not hemispheres (unless the special case where cylinder is infinitely thin and so the plane cuts right through the center of the sphere). What is the volume of one of these caps? Rather than derive it here, I'll look it up on Wikipedia 
With some algebra this can be rearranged to give an equation without the smaller radius. 
|
Martin Gardner Puzzle
This segues perfectly into a Puzzle that is, arguable, one the Martin Gardner's most famous puzzles:(It's also sometimes referred to as "The Napkin Ring Problem")
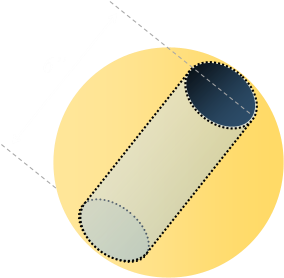 |
“A six inch high cylindrical hole is drilled through the center of a sphere. How much volume is left in the sphere?” That's it! No more information is given! |
No mention is given to the size of the sphere, no mention is given to the diameter of the hole. How can an answer possibly be determined? Let's give it a go and see …
The solution to the problem is to start with the volume of the sphere, and from this subtract the volume of the cylinder, then the volume of two spherical end caps. Whatever is left is the solution.
From the puzzle definition h = 6, and the 'height' of the cap c = R-3.
Substituting these in we get the following:
|
|
Expanding out, we find that lots, and lots, of things cancel …
… until we reach the staggering result: The volume of the 'ring' left is 36π (cubic inches).
The arguments for the radius of the sphere and the hole diameter have all cancelled out.
The result
 |
That's right, the solution is agnostic of the diameter of the sphere. We could have a sphere as large as a planet, bore a hole 6" in length through it (it would be a pretty wide hole!), and the volume of the earth left in the ring around the edge would be 36π cubic inches. This is a very neat answer, and you can see why Mr Gardner liked it so much. |
Cheat Answer
I've heard an alternate mechanism of solving this problem. It's a bit of a cheat:
The problem would not be given unless it has a unique solution. If it has a unique solution, the volume must be a constant which would hold even when the hole is reduced to zero radius. Therefore the residue must equal the volume of a sphere with a diameter of six inches, namely 36π.
More Martin Gardner Puzzles
If you liked this puzzle, check out some other Gardner inspired Counter-intuitive Conundrums.
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.