Intransitive Dice*
(*How to win free drinks from your friends)
I predict this posting (similar to my recent postings about Benfordís Law and Counterintuitive Conundrums) is initially going to generate a lot of “No way!” and “That canít possibly be true!” comments.
Hold on tight and I'll show you how you can use math to wager free drinks from your friends …
Dice Game
Letís play a dice game. I have three dice (shown below). They are similar to regular six-sided dice except they have slightly different numbers on them. Each die is different. Iíll label them Red , Green and Blue so that we can differentiate them.

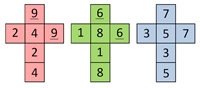 |
The meshes for the three dice are shown here on the left. Rules – Weíre each going to choose and roll one of the dice. Iíll even let you choose first. You are free to select any die you like (Red, Green or Blue), then Iíll pick one of the two remaining dice. We then enter into a battle: We both roll our dice, and the highest scoring number wins a point. Weíll roll twenty times and declare a winner as the one with the most points. Simple? |
|
It might not be a surprise to my suspicious readers, but Iím going to predict that Iím probably going to win the battle. In fact Iíll go as far to say that I think Iíll win the battle over 61% of the time (Even if, in the event of a tie at ten points each, I concede the win to you). OK, you say, I somehow forced you into picking one of the dice? No problem, letís do it again. |
 |
 |
You can chose to keep the same die, or select another one (you can even have the die I just rolled if you like!) I predict Iím going to win again. We can keep going all day. It does not matter which of the dice you choose, Iíll select one of the other dice and win over 61 times in every 100 games. Huh, whatís going on? That does not make sense! Whatís the trick? Thereís no trick, itís just that youíre thinking in a transitive way (donít worry Iíll explain what that means shortly). Want to know more? Read on … |
How to Play
First, Iím going to explain the strategy of how I play. Then, Iíll explain why it works:
|
If you select the Red die, Iíll select the Blue one (and probably win). If you select the Green die, Iíll select the Red one (and probably win). If you select the Blue die, Iíll select the Green one (and probably win). |
Yes, it's that simple!
You might want to go away and make a set of these dice for yourself to use as you read this article (and then use them to scam your unwitting friends out of free drinks by betting against them).
Intransitivity
So, whatís special about the dice? Well nothing really. They are striped with numbers, but why this ĒtrickĒ works is that the relationship ĒIs more likely to roll a higher numberĒ is intransitive.
|
What does that mean? A Transitive function or property is something in which all comparisons are performed according to the same dependent criteria. For example, if Albert is older than Bob, and Bob is older than Charlie, then we know that Albert must be older than Charlie too. This is because "is older than" is a Transitive function. However, if I told you that Albert is friends with Bob, and Bob is friends with Charlie, you canít assume that Albert is also friends with Charlie! Friendship is Intransitive. For our dice set, the function "Is more likely to roll a higher number" is intransitive. |
 |
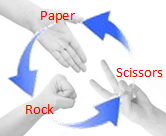 |
Need more convincing about the concept? At first glance this may appear counter-intuitive, so let's look at the classic game of Rock-Paper-Scissors, which is also an intransitive game. Rock smashes Scissors, and Scissors cut Paper, but Paper also wraps Rock. If you are playing Rock-Paper-Scissors and you know which symbol your opponent was going to select, you could always select the device that was its nemesis and be sure of a victory. Get it? OK, let's go back to the dice … |
|
Our dice are constructed in a similar cycle such that the value "Is more likely to roll a higher number" sequences around in a loop.
Red is more likely than Green Green is more likely then Blue Blue is more likely than Red . Because I asked you to select your die first, I can always select the color next along the cycle! |
 |
Math
Now that we have the background out of the way, let's look at some numbers. By it's nature, rolling dice is random and we can exploit that with our function "Is more likely be higher".
Below are the meshes for the dice we are using for this example:
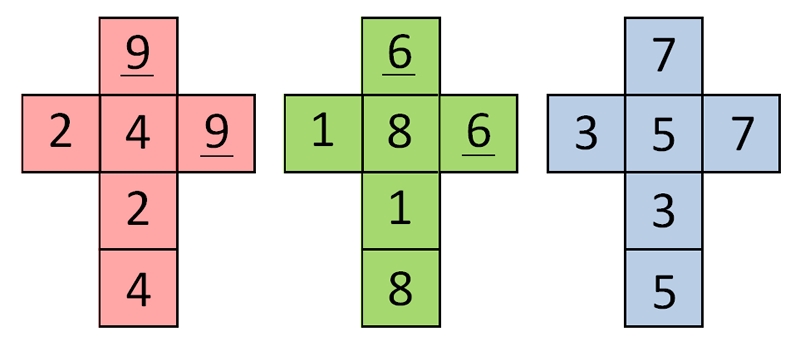
If you look closely, you will see that each dice has just three distinct numbers (repeated twice).
The Red one: 2,4,9. The Green one: 1,8,6 and the Blue one: 3,5,7.
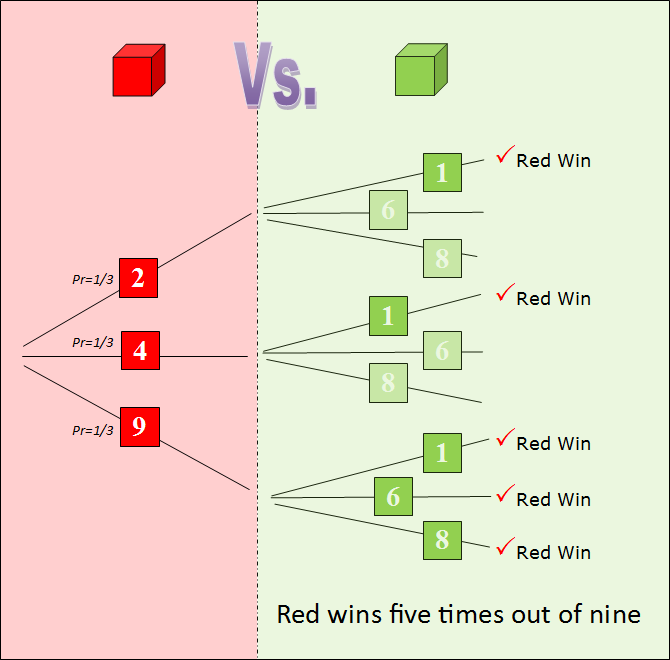
Rolling the red die, there are three equally likely outcomes (each with Probability 1/3). The same can be said for the green die.
Multiplying these together, we see that there are nine possible (equally likely) outcomes for these pair of dice. In five of these combinations the red die wins. Thus, probablity of the red die winning against the green die is 5/9. This is shown below as a tree diagram:
 |
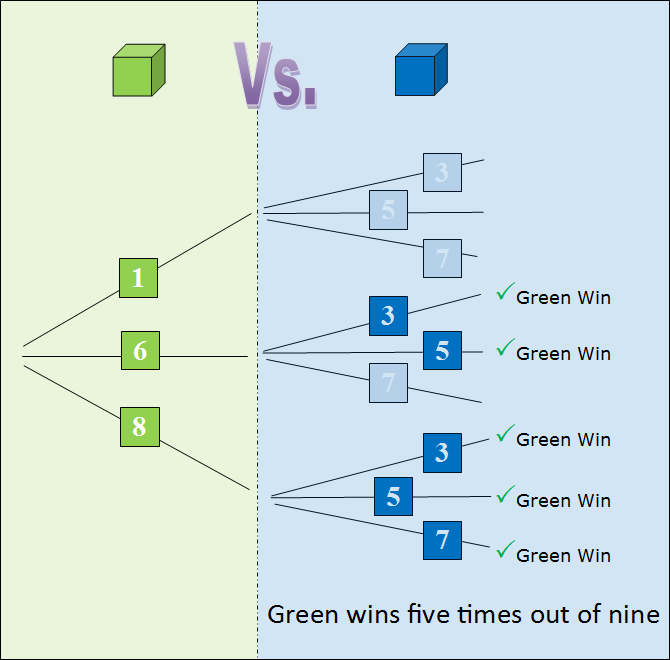
A similar diagram can be constructed for all possible combinations of rolles for the green and blue dice. Again the probability is weighted, and again the advantage is 5/9.
 |
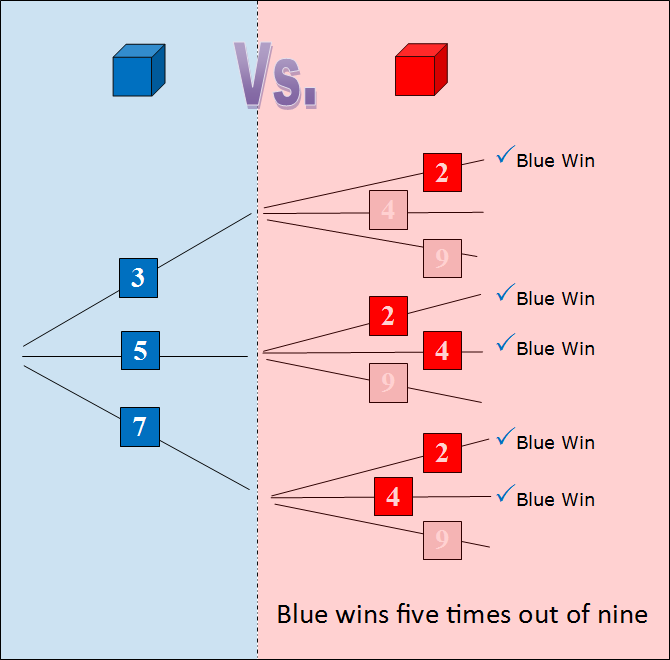
Finally, with the blue and red dice we can again complete the cycle with a 5/9 probability.
 |
By selecting the correct die against one freely selected by our opponent we can gain always gain a measurable advantage.
The 5/9 advantage is small, but by repeating the experiment a few times (in our example by repeating the roll twenty times), we can increase our odds considerably.
Go out and have fun with math!
More Dice Fun – Why stop at three?
It's perfectly possible to construct loops of higher orders than three. There's a famous set of four named Efron's Dice after statistician Bradley Efron. Here are his numbers:
Dice 1: 4 4 4 4 0 0
Dice 2: 3 3 3 3 3 3
Dice 3: 6 6 2 2 2 2
Dice 4: 5 5 5 1 1 1
With Efron's Dice, each die is beaten by the previous die in the list with a probability of 2/3.
There are many other combinations, for instance look at these two sets. Interestingly, in the two examples show below the Expected Value of each die is the same (The average over many rolls). In my line of business, you have to be really careful examing data; you have to really understand what you are looking at. If you just looked at the average roll of these dice you might draw the conclussion that they are exactly the same!
|
Dice 1: 7 7 7 7 1 1 Dice 2: 5 5 5 5 5 5 Dice 3: 9 9 3 3 3 3 Dice 4: 8 8 8 2 2 2 |
Dice 1: 6 6 6 6 0 0 Dice 2: 4 4 4 4 4 4 Dice 3: 8 8 2 2 2 2 Dice 4: 7 7 7 1 1 1 |
I've seen other sets containing five dice. These are even more interesting as they contains more than one intransitive loop allowing you to, potentially, wager against more than one person at the same time; once you've learned the cycles, and win free drinks at twice the rate!
Nearest to 'normal' dice (Geeks Only)
If you're a purest, and want to use dice that look as similar to 'normal' dice as possible, might I suggest this set of three?
Dice 1: 1 1 3 5 5 6
Dice 2: 2 3 3 4 4 5
Dice 3: 1 2 2 4 6 6
This set uses just the regular numbers [1-6] found on a 'normal' die.
The probability of winning around the cycle is 17/36 (which is not in your favor!), but there is a probability of a tie at 4/36. Ties never occured in our first set (each number was distinct), so if you modify the rules such that a tie requires both parties to re-roll, you can shift the odds to your favor as you only lose on 15/36 rolls (Evil snigger!)
Geek Trivia – For the dice sets above, did you know that the spot count of each dice is still 21 (which is the same spot count as a 'normal' die [1-6]?)
If you are making a set of these, if you are careful, you only need to make two changes on each die:
Dice 1: Change the 2 to a 1, and the 4 for a 5.
Dice 2: Change the 1 to a 3, and the 6 for a 4.
Dice 3: Change the 3 to a 2, and the 5 for a 6.
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.