Why are cans shaped the way they are?
|
The purpose of a food can is to store food. It costs money to manufacture, store, and ship these containers. One would imagine, therefore, that over time a lot of thought has gone into their design and production. One would hope that, as billions of food and beverage cans are manufactured every year (yes, that's a “B”), the current designs are optimal for their purpose. If not, as a planet, we’re wasting a lot of energy manufacturing sub-optimal designs. So then why are cans cylindrical tubes? And why do they have the aspect ratios they do? (Ratio of height to diameter) |

|
Why cylindrical tubes?
 |
If the goal was to purely maximize the volume of food that could be stored in a container, the result would be a spherical can. A sphere is the shape with the minimum surface area to volume ratio. It could contain the most amount of food for the least amount of can material. However, it would be totally impractical! It would not stay still on a shelf, making display and storage hard. How would you hold it? How would you open it? How could you manufacturer and fill it? When stored in packing boxes, even with hexagonal close packing there would be unused gaps in the storage boxes. |
Clearly optimizing purely based on minimizing the material needed for an individual can is not optimal.
|
If we wanted to use a shape that packed perfectly efficiently, we’d use some kind of cuboid. These would sit and stack nicely on shelves too. They’d be easier to manufacture than spheres, but the edges would be stress points. You occasionally seen cuboid-like containers (corned-beef, spam and sardines are the first that come to mind). Rather than sharp edges, these have filleted (rounded) edges to reduce stress concentrations and to make them easier to manufacture. |
 |
Taken to the limit, a cube would be the most efficient of the square cornered containers. I’ll not prove it here, but a cube is the format that minimizes the surface area to volume ratio of a cuboid. But we don’t see many cubes on shelves. Let's look at cylinders now …
 |
Cylinders are relatively easy to manufacture. In the past they were manufactured by cutting a rectangle of material and wrapping this around with a single seam weld to which two circular end caps were attached. (Modern aluminum cans are made in two pieces; the first is a combined bottom/side punched and extruded into a cup shape, and the second is a circular cap attached to the end). Being round in section, they have no corners in the hoop-plane and so minimize the stress concentrations when the can is under pressure (storing carbonated beverages, or during the cooking of the food in the cans). See Why do pipes burst for more details on this calculation. |
Cylindrical cans stay put when you put them on a shelf, and they are relatively easy to open with a simple can opener (and when opened still stay put and the contents do not spill out). When packed in boxes, even though not as efficient as cuboids, they pack more efficient than spheres (Approx 79% cf. 74%).
But what aspect ratio (Height to Diameter ratio) is the best to use, and why?
Audit
Let’s pause for a second whilst I audit my pantry. This is not an exclusive list of sizes, nor is it intended to be a complete list. It just happens to be a selection of random cans that were there when I looked.

Here is a table of their diameters and heights from left to right:
| Name | Diameter | Height |
|---|---|---|
| Chicken Broth | 75 mm | 105 mm |
| Condensed Soup | 65 mm | 98 mm |
| Tuna | 85 mm | 40 mm |
| Condensed Milk #1 | 75 mm | 94 mm |
| Condensed Milk #2 | 74 mm | 77 mm |
| Chunky Soup | 85 mm | 107 mm |
| Almonds | 84 mm | 57 mm |
Now for a little math refresher
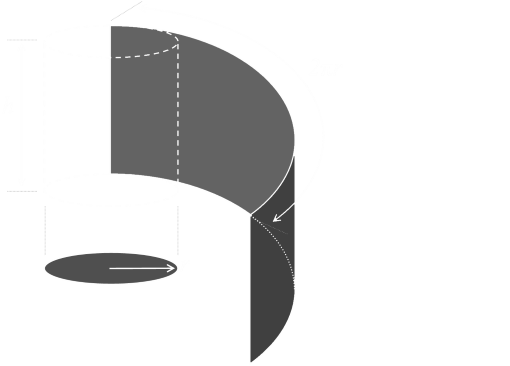 |
The volume of a cylinder is the area of the cap, multiplied by the height: 
The surface area of a cylinder is area of two of the circular end caps, plus the rectangle that wraps around the edge forming the sides. 
|
If we divide the volume of each can by the surface area of each can, this will tell us the ratio of these values, but it will not tell us what the optimal shape is for the volume of food held. To do this, we need our old friend Calculus.
Optimal can size
To work out the optimal size, we keep the volume of the cylinder fixed, then find the relationship between the radius and the height.
Recall the simple formula for the Volume, and we can re-arrange this to get an equation for the height:
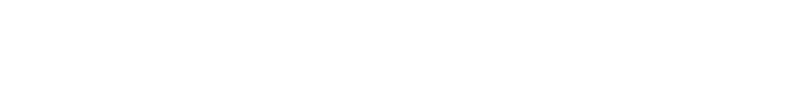
We're trying to minimize the surface area, and here is the equation for this, into which we will substitute the equation for the height:
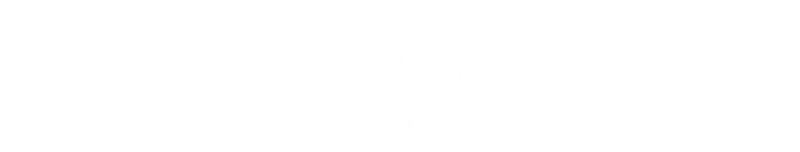
Next we find the first derivative of this and set it to zero to find the turning points in the function:
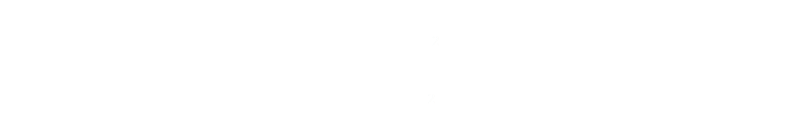
(The second derivative is positive, confirming that this turning point is a minimum). We now have a relationship between the volume and the radius for the minimum surface area. Finally substituting back for the valuation of h reveals the result:
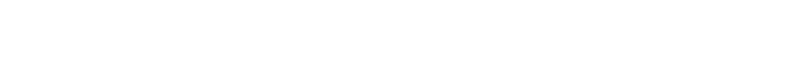
The most efficient can is one where the height is twice the radius (which of course is the diameter).
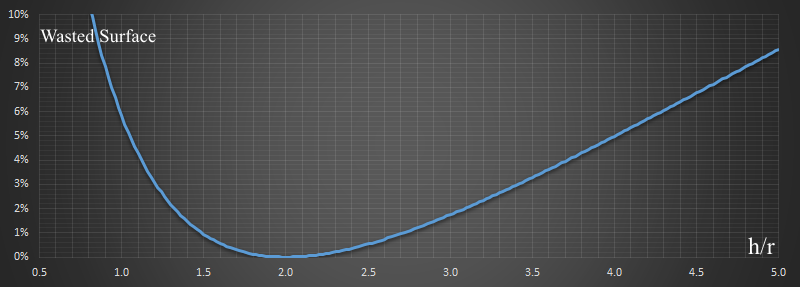
Plotting it out
Below is a graph of how much material (surface area) cans of variable aspect ratio require. On the x-axis is plotted the ratio of h/r (the height to radius ratio). As we can see, the graph has a minimum at h=2r (when the height is the diameter). This is what we calculated with our Calculus. Tall skinny "Pringle" can like cans are on the right, and short flat "Pancake" like cans are on the left.
On the y-axis I've plotted the efficiency of the can by showing a normalized value of the excess material needed (as a percentage of the minimum surface area). Cans that have a higher, or lower, aspect ratio than the optimal require more surface area to contain the same volume (and thus more material).
Plotting out my cans
Here is my table of cans with additional columns added. For each row I've added the the h/r ratio, and also a column to show how inefficient that can is compared to the optimal can that would hold the same volume of goods:
|
 |
Here's the data plotted on the curve:
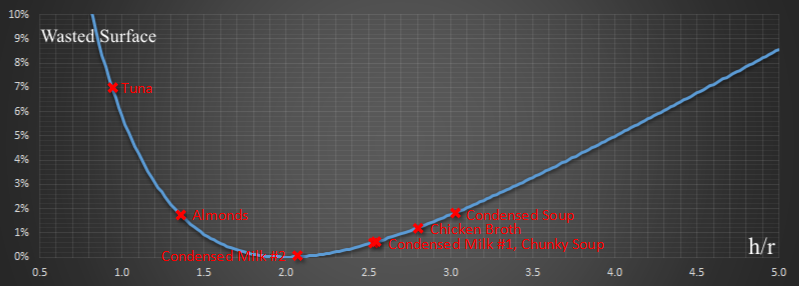
Out of all the cans in my pantry, the tuna is the most inefficient, and the condensed milk #2, Eagle Brand, is pretty close to the perfect ratio. Well done guys! Your product is sold in the most efficient can possible.
So why not everyone?
|
The math above isn't hard. I'm sure more people than the good folks at Eagle Brand have done the calculations for optimal efficiency. Why don't others make their cans the same aspect ratio and save all that inefficient use of material? I'm not an engineer at any of their plants, but here is some speculation on my part. Believe as many as you like (some are more convincing than others!): 
|
 |
For the almond tin, we can give some leniency. This container is designed to allow fingers to dip in and pick up nuts to eat. If the diameter were too narrow (or the container too deep), then fingers would not be able to get inside.
Aesthetically, a slightly taller can looks nicer. The Golden ratio is approx 1.6, so a can with a height of approx 1.6x it's diameter (3.2x the radius) would be very appealing. This corresponds very closely to the condensed soup can ratio.
Cans (especially drinks ones) are designed to be held in the hand. If the diameter is too large, it's hard to hold them (either to drink or open them). There's an obvious maximum diameter that an adult hand can hold, after that, if you want to increase the volume you have to make the container taller.
To open a can, a cutting device has to revolve around the rim. The larger the diameter of a can, the more effort and work is required to open it.
Our above, simple, calculations make the very basic assumption that all parts of the can are equal. This, clearly, is not the case. The end caps of the can could be made of different thickness material that costs a different amount of money per unit area. There is no reason why it should cost the same.
Related to the above, the end caps are circular, whilst the sides are cut from rectangular stock. The sides can be cut with no wastage. Circular caps need punching out of stock leaving material behind. This, obviously, will be recycled, but the manufacturer has had to pay for processing the raw material into the sheets from which the circular blanks will be cut. This is a waste of energy. Even if they were the same material stock as the side, they would cost more to manufacture.
There is more to manufacturing than just the cost of the raw material. There is the cost of welding (both the seam of the can, and the two end caps). Depending on the relative price of generating a weld per unit length (and/or the cost of circular welds against straight welds), compared to the cost of raw material, a different shape could be more efficient.These days most cans are punched from aluminium blanks, not welded, but a similar argument can be applied: There are more costs in manufacturing than just the costs of the raw material.
Familiarity. The original cans may have been manufactured with an arbitrary aspect ratio, but now we've been programmed to search for items of this shape when we shop. A soup can of the wrong shape might not attract our attention (or bizarrely might be less attractive) to shoppers. Changing a can shape at this stage (without accompanying large budget media awareness campaigns) could have a negative impact on sales
Cans are not manufactured or sold singly, but are packed in boxes/crates. Depending on can size and crate size, and the configuration of packing, some configurations might use different quantities of packing material (though typically, this will be cheaper than the can material).
You can find a complete list of all the articles here. Click here to receive email alerts on new articles.
Click here to receive email alerts on new articles.